7 клас

Дистанційне навчання з 12.10.21.

Алгебра

Он-лайн урок 17.11.21

Тема: Множення одночлена на многочлен.

👉І. Математичний диктант

Варіант 1	Варіант 2
1. Запишіть рівність, яка виражає розподільний закон множення щодо

додавання	віднімання
2. Запишіть вираз:
різниця чисел 40 і 1, помножена на число 9	сума чисел 30 і 6, помножена на число 5
Знайдіть його значення, використовуючи розподільний закон
3 . Запишіть вираз:
577 ∙ 58 + 423 ∙ 58	768 ∙ 95 - 668 ∙ 95
Знайдіть його значення, використовуючи розподільний закон
4. Запишіть вираз:
15(2+x)	(3+у)12
Перепишіть його по-іншому, використовуючи розподільний закон

👉ІІ. Письмове. 

1) Підручник. Вівчіті п.10, с.65-66, №355 (1-6), 357 (1-4).
2) Приклади 1; с. 65. 

👉ІІІ. Домашнє завдання. Вівчіті п.10, с.65-66, №356 (непарні), 358.

Геометрія.

Урок 16.11.21

Тема: "Паралельні та перпендикулярні прямі. Контрольне тестування"

👉І. Усно. 

1. Повторити п. 4-9. Уроки 12.10.21 – 11.11.21

👉ІІ. Письмове.

1. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSf5ro3biwnqk-MKS-6lWUFyChLnL0spedoSSk8aDYUJ0ae-TQ/viewform?usp=sf_link

👉ІІ. Домашнє завдання. 

Повторити п. 4-9. Письмово розв'язати тестові завдання.

Алгебра

Он-лайн урок 12.11.21

Тема: "Степінь з натуральним показником. Одночлен. Багаточлен.

👉І. Усно.

1. Подайте у вигляді степеня вираз:  a 2 · a  6  

2. Подайте у вигляді степеня вираз:  b 15 : b  12  

3. Подайте у вигляді степеня вираз: ( c 2 ) 10

4. Вказати правильні рівності: 

                 а20 : а4 = а16

 

           а20 : а4 = а5

 

           а20 ⋅ а4 = а80

 

           а20 ⋅ а4 = а24

 

           (а12)2 = а24

👉ІІ. Письмово.

1. Знайдіть значення виразу:   3,5 · 23 – 93  .

2. Спростити вираз:  (–3x2 + 2x – 3) – (x2 – x – 14)

3. Спростіть вираз:  (–0,2 x y4 )2 · (–4) x2 y2
 

4. Замість зірочки вставте такий многочлен, щоб утворилася тотожність: 

(24 x8 – 12 y z + 4 y2 ) – ( * ) = 6 x8 – 10 y z + y2 .

5. Звести многочлен -7х2 - 3х - 6х2 + 8х -10 до стандартного вигляду.

6. Знайти значення многочлена: - 4х2 - 2х, якщо х = - 3.

👉ІІІ. Домашнє завдання. Повторити п.4-9. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSczjpHFng_3DrDXsg0_Iy8rOrFq7HVgePRVsTJ6qIuSvvP63w/viewform?usp=sf_link

Геометрія.

Урок 11.11.21

Тема: "Паралельні та перпендикулярні прямі. Підготовка до контрольного тестування"

👉І. Усно. 

1. Теоретичні питання. 

1) Які кути називають суміжними? 

2) Чи правильно, що: 

- Якщо два кути суміжні, то їх сума дорівнює 180; 

- Якщо сума двох кутів дорівнює 180, то вони суміжні? 

3) Які кути називають вертикальними?

4) Чи правильно, що: 

- Якщо кути вертикальні, то вони рівні;

- Якщо кути рівні, то вони вертикальні?

5) Які прямі називають паралельними?  Які прямі називають перпендикулярними?

6) Пряма а паралельна прямій b, а пряма b перпендикулярна до прямої с. Яке взаємне розміщення прямих а і с?

7) Чи можна зробити висновок, щодо паралельності двох прямих, якщо відомо, що в результаті перетину цих прямих січною утворилися: 

- Внутрішні односторонні кути, сума яких дорівнює 160;

- Внутрішні різносторонні кути, сума яких дорівнює 160;

- Внутрішні односторонні кути, сума яких дорівнює 180;

- Внутрішні різносторонні кути, сума яких дорівнює 238, один із них — 119;

- Рівні відповідні кути;

- Внутрішні односторонні кути рівні й дорівнюють по 90?

8) Дано пряму a і точку B, що не лежить на прямій a. Скільки прямих: 

а) можна провести через точку B;

б) що перетинають пряму a, можна провести через точку B;

 в) паралельних прямій a, можна провести через точку B? 

9) Дано прямі a і b, що перетнуті прямою c (рис. 2).

Що треба знати про кути:

а) 3 і 5; б) 3 і 6; в) 2 і 6; г) 1 і 8; д) 1 і 6, щоб зробити висновок, що a||b?

3) На рисунку 2: ∠3 = ∠ 6. Що при цьому можна сказати про кути 4 і 6; кути 1 і 5. Чому?

👉ІІ. Письмово.

1) Дано дві прямі, що перетинаються:

а) Скільки кутів при цьому утворилося?

б) Сума двох кутів, що утворилися, дорівнює 100°. Які це

кути? Знайдіть їх.

в) Один з кутів удвічі більший за інший. Які це кути? Знайдіть їх.

2) Градусна міра одного з кутів, що утворилися при перетині січною двох паралельних прямих 140 градусів. Знайти градусну міру решти семи кутів. 

3) За даними рисунка 3 знайдіть кути 1 і 2, якщо a||b.

👉ІІ. Домашнє завдання. 

Повторити п. 4-9. Розвязати задачі.

1. При перетині двох прямих утворилося чотири кути. Чи можуть деякі два з них дорівнювати:

А. 5 º і 175º; Б. 15ºі 19º; В. 27ºі 154º; Г. 3ºі 3º.

2. Один з кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 37 градусів. 

Чи може один з решти семи кутів дорівнювати: 

А) 133, Б) 143, В) 153.

3. Сума двох кутів, що утворилися при перетині двох прямих 142 º. Знайти всі кути, що утворилися.

 

4. Знайти кут між прямими, що перетинаються, якщо сума трьох з утворених кутів 293 º. 

5. Кут ABC дорівнює 62°, а кут BCD дорівнює 118°.

Чиможуть прямі AB і CD:

а) бути паралельними; б) перетинатися?

6. На площині проведено прямі a, b і c, причому a||b, а 丄 с Визначте взаємне розміщення прямих b і c.

7. Знайдіть усі кути, утворені в результаті перетину двох паралельних прямих січною, якщо:

а) один із внутрішніх односторонніх кутів на 30° більший, ніж інший;

б) сума двох відповідних кутів дорівнює 56° 

Он-лайн урок 09.11.21.

Тема: "Властивості паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною. Розвязування задач".
👉І. Усно.

1. Знайдіть усі невідомі кути на рисунку 1, якщо a||b:  

_{а) ∠1 = 20, б) ∠1 = ∠2, в) ㄥ1 =  3 * ㄥ2.}
 
 

2. Дано: AB || CD, BC || AD (рис. 2). Доведіть, що ∠1 = ∠2, ∠3 = ∠4.

3. Укажіть взаємне розташування прямих b і c, якщо a||b, с⊥а.

👉ІІ. Письмово.

1. За даними рисунка 3 знайдіть кут x.

2. Січна перетинає дві прямі; при цьому утворилися кути 1, 2 і 3. Відомо, що кути 1 і 2 — внутрішні різносторонні, а кути 2 і 3 — вертикальні. Як розміщені один відносно одного кути 1 і 3?

3. Дано a||b. Знайдіть ∠1, ∠2.

4. За даними рисунка 6, визначте, чи паралельні прямі a і b, якщо ∠2 - ∠1 = 54o.

5. Бісектриси внутрішніх односторонніх кутів, утворених у результаті перетину двох паралельних прямих січною, взаємно перпендикулярні. Доведіть.

👉ІІІ. Домашнє завдання. Повторити п.4-9, "Контрольні запитання" 1-9, с.70. Письмово №264, №266, №274 (2).

Алгебра.

Урок 05.11.21

Тема: "Цілі вирази. Розвязування задач"

👉І. Усно. 

1. Повторити п.4-9, с.27-59.

2. Яка з рівностей є  тотожністю?

а) -3(а-с)=-3а+3с;

б) 9а-8а+а=2а;

в) 8а-(4а+1)=4а-1;

г) -(х+3у)+(2х-у)=3х+2у.

3. Який з виразів є одночленом?

а) 0,4х+у;

б) 0,4х-у;

в) 0,4ху;
г) немає жодного.

4. Повторити формули

an⋅am=an+m

an:am=an−m

1) Подайте у вигляді степеня з основою х вираз:

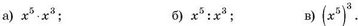2) Піднесіть до степеня добуток: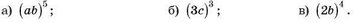3) Знайдіть значення виразу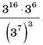  

👉ІІ. Письмово. 

1) Підручник №312 (1), 314 (1).
2) Приклади 1; 2; 3 с. 58-59. 

👉ІІІ. Домашнє завдання. Повторити п. 4-9, Письмово завдання №2 "Перевір себе" в тестовій формі (2-4; 6; 7; 9-12).

Геометрія.

Урок 04.11.21.
Тема: "Властивості паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною".
👉І. Усно.

1. Дано пряму a і точку B, що не лежить на прямій a. Скільки прямих:
а) можна провести через точку B;
б) що перетинають пряму a, можна провести через точку B;
в) паралельних прямій a, можна провести через точку B?
2. Дано прямі a і b, що перетнуті прямою c (рис. 2).

Що треба знати про кути:
а) 3 і 5; б) 3 і 6; в) 2 і 6; г) 1 і 8; д) 1 і 6, щоб зробити висновок, що a||b?
3. На рисунку 2 Що при цьому можна сказати про кути 4 і 6; кути 1 і 5. Чому?

👉ІІ. Вивчення нового матеріалу.

1. Таблиця

2. Підручник. Вивчити п.9, с.63-66. Відповісти на запитання 1-5 "Пригадайте головне", с.66. 
3. Розвязати задачі.

Самостійна робота
1. Січна перетинає дві прямі; при цьому утворилися кути 1, 2 і 3. Відомо, що кути 1 і 2 є вертикальними, а кути 2 і 3—внутрішні різносторонні. Як розміщені один відносно одного кути 1 і 3?
2. Дано a||b (див. рис.). Знайдіть ∠1 ; ∠2.

3. Чи правильно, що коли при перетині двох прямих січною утворилися чотири гострі та чотири тупі кути, то дані прямі є паралельними?
4. Січна перетинає дві дані прямі; при цьому утворилися внутрішні односторонні кути, один із яких дорівнює 45°, а інший у 3 рази більший. Доведіть, що дані прямі паралельні.

👉ІІІ. Домашнє завдання. Вивчити п.9, с.63-66. Відповісти на запитання 1-5 "Пригадайте головне" (с.66), №262, №265, №267 (1).

Алгебра

Урок 03.11.21

Тема: "Додавання і віднімання многочленів"

👉І. Усно.

1. Перевірка д/з.

👉ІІ. Вивчення нового матеріалу.

1. Підручник п.9, с.58-59.

2. Конспект.

3. Письмово №306, №308 (1; 2).

👉ІІІ. Домашнє завдання.

1. Вивчити п.9,  с.58. 2. Розв’язати: №309(1,2), №312(1), №314(1).

Урок  02.11.21

Тема. Ознаки паралельності прямих.

👉І. Усно. 

1. Повторити п.7 (урок 28.10.21)
2. Вивчити п.8, с.58.
Теорема (ознака паралельності прямих).

Якщо при перетині двох прямих січною виконується принаймні одна з умов:

- внутрішні різносторонні кути рівні;

-сума внутрішніх односторонніх кутів дорівнює 180 градусів;

- відповідні кути рівні,

то дані прямі паралельні.

3. Приклад 1. Якщо внутрішні різносторонні кути рівні (див. рис.), ∠3=∠5, то а॥ b, с-січна.

 

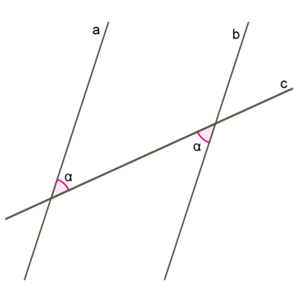
4. Наслідки 1,2,3.
Ознаки паралельності прямих на площині.
 -  Дві прямі, паралельні третій, паралельні між собою.
 -  Якщо дві прямі на площині перпендикулярні до однієї й тієї самої прямої, вони паралельні.

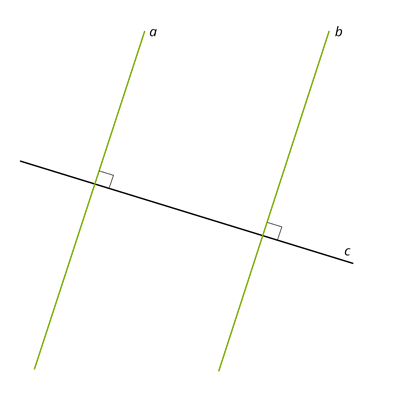
5. Задача с.60.
6. Відповісти на запитання 1-4 "Пригадайте головне".
7. Виконати: №235,№240, №242.

👉ІІ. Письмово.

1. Відомо, що дві паралельні прямі перетинає січна. ㄥ1=135 градусів. Знайти інші кути.

 

2. Підручник п.8, №237(1,2), №241(1,3), №243(1,2), №246(1).

👉ІІІ. Домашнє завдання. Вивчити п.8, виконати №239, №244, №247.

Урок 29.10.21

Тема:"Многочлени"

👉І. Усно.

1. Які з виразів:
bа + b; 8а 2 -3k 3 ; 0,2сd 7 ; 66; 3 - с 2 
є одночленами?
2. Які одночлени називають подібними? Наведіть приклади.
3. Зведіть подібні доданки:
а) -9х + 7у - 5х + 2у; 
б) 5а 2 - 6а + 2а 2 + 10а;
в) 23р 2 -23 + 4к 2 + 4р 2 .
4. Подайте у вигляді суми вираз:
а) 7k – 4b; б) -9b 2 а - аb 2 .
👉ІІ. Вивчення нового матеріалу.
1. Підручник. Вивчити п.8, с.54-55.
2. Відповісти на запитання 1-5, с.55.
3. Усно №292.
4. Письмово №293(1; 2), №295 (непарні), №297(1).
👉ІІІ. Домашнє завдання. Вивчити п.8, с.54-55, №294; №296, №298 (1).

Геометрія

Урок  28.10.21.

Тема: Паралельні прямі. Кути, утворені при перетині двох прямих січною.

👉І. Усно.

1. Повторити п.6 (с.48), "Пригадайте головне".

👉ІІ. Вивчення нової теми.

1. Вивчити п.7 (с.52-55).

2. Відповісти на запитання 1-5 (с.55)

3. На рисунку назвіть прямі, що перетнуті січними; січні; пари відповідних кутів при прямих  m i n i січній k; при прямих m i n i січній р.

4. Письмові вправи.

1) Запишіть задачу (с. 54) у зошит.
2) Виконайте №115, №221 за зразком.

👉ІІІ. Домашнє завдання.

Вивчити п.7 (с.52). Виконати №219, №224(1,2), №225(1,2).

Урок 27.10.21.

Тема: "Одночлени"

👉І. Усно.
1. Підручник с.47, №258, №259.
👉ІІ. Вивчення нового матеріалу.
Підручник п7, с.47-49.
1) Означення. Що називають одночленом?
2) Що таке степінь одночлена?
3) Приклад 1.
4) Приклад 2.
5) Відповісти на запитання 1-5 (с.49).
6) Усно №261-263.
👉ІІІ. Письмово. №265, №267, №271.
👉ІУ. Домашнє завдання. Вивчити п.7, с.47-49, №266, №268, №272.

Геометрія

Урок 26.10.21.

Тема: "Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої"

👉І. Усно.

1. Вивчення нового матеріалу.

Підручник п.6, с.45-48. ☝"Пригадайте головне" 1-6.

2. Теорія.

Дві прямі, що перетинаються під прямим кутом, називаються перпендикулярними.

 

  

Скорочено це записують так: a⊥b

Відстанню від точки до прямої, яка не проходить через дану точку, називається довжина перпендикуляра, проведеного з даної точки до даної прямої.

Перпендикуляром до даної прямої a, проведеним із точки A, називається відрізок прямої, перпендикулярної до даної, одним із кінців якого є точка A, а другим (основою перпендикуляра) — точка перетину цих прямих C.

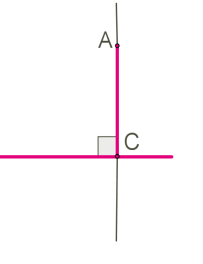
Теорема про існування і єдиність перпендикуляра до прямої.

Від точки, що не лежить на прямій, можна провести перпендикуляр до цієї прямої, причому лише один.

  

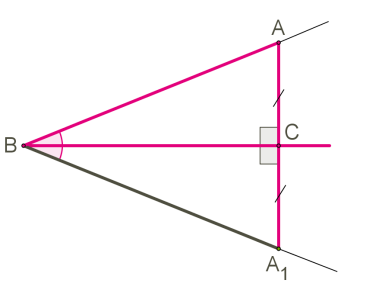
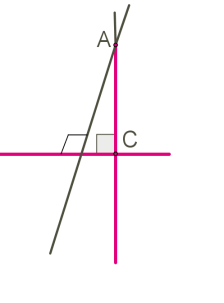
👉ІІ. Письмово.

Підручник с.48, №188, №191, №№195 (мал.120), №196 (1).

👉ІІІ. Домашнє завдання. Вивчити п. 6, №197, №199.

Алгебра.

Урок 15.10.21.

Тема: "Розвязування задач. Самостійна робота".

👉І. Усно.

1. Подайте у вигляді степеня з основою х вираз:

 
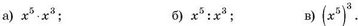
2. Піднесіть до степеня добуток: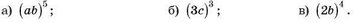3. Знайдіть значення виразу
  
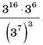
👉ІІ. Письмово.
1. Опрацювати приклади1-4 (підручник п.6, с.41-42).
2. Самостійна робота.
 
1) Подайте у вигляді степеня добуток: 2) Піднесіть до степеня степінь:
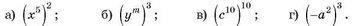 3) Піднесіть до степеня добуток:
 4) Знайдіть значення виразу:
 

👉ІІІ. Домашнє завдання. Повторити п.6 (формули), №209, №216, №222.

Урок 13.10.21.

Тема: "Властивості степеня  з натуральним показником".
👉І. Усно. 

1) Заповніть пропуски

- Добуток, що складається з однакових множників, називається ____.

- У виразі aⁿ, число а-_____, число п -_____.

- Якщо показник парне число, то значення степеня завжди _____.

- Якщо показник непарне число, то значення степеня завжди ___.

2) Записати вираз у вигляді степеня? 

Назвіть основу й показник: 

1) 4·4·4·4·4; 2) (-2)·(-2)·(-2); 3) ···; 

4) (ab)(ab)(ab);  5)(а – b)(а - b);  6) х·х·х·у·у·у·у;  

7) .

👉ІІ. Вивчення нового матеріалу.

1) Підручник п.6, с.39-42 . Вивчити теореми 6.1-6.4.

2) Записати властивості степеня з  натуральним показником (формулии, форзац 2).

an⋅am=an+m

an:am=an−m

3) Записати приклади на застосування формул (після кожної теореми).

4) Приклад 1. Запишіть відповідь у вигляді степеня з основою с і ви дізнаєтеся прізвище та ім'я великого французького математика.

Ключ:

5) Приклад 2.

Натисніть на посилання. Продивіться відео.

https://youtu.be/jQ1OOe0a7lA

👉ІІІ. Домашнє завдання. Вивчити теоретичний матеріал п.6 (ст.39-41), №205(1-4), №210, №214, №232.

Геометрія

Урок 12.10.21.
Тема: Суміжні та вертикальні кути. Тест контроль".

👉І. Усно.

1. Знайдіть кут, суміжний з кутом 30°; 90°; 120°;α(0^o<α<180^o).
2. Визначте на рисунку 3 види кутів, що утворились:
1 і 2... 2 і 3...
1 і 3... 2 і 4...
1 і 4... 4 і 3...

3. Визначте вид двох з кутів,що утворились при перетині двох прямих, якщо:
а) один з них на 20° більший за інший;
б) їх сума дорівнює 100°.

👉ІІ. Письмово.

1. Один із кутів, що утворилися в результаті перетину двох прямих, дорівнює 125°. Знайдіть решту кутів. Чому дорівнює кут між цими прямими? (Дивись рис. 3)

☝Означення. Кутом між двома прямими , що перетинаються, називають гострий кут.

2. Знайдіть усі кути, що утворилися в результаті перетину двох прямих, якщо:
а) сума трьох із них дорівнює 295°;
б) градусні міри двох із цих кутів відносяться як 4 : 5 (Дивись рис.3).

👉ІІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSck2rCm7E_WhdMRZEFYSTZ9lGNHyxiKPXMyDXGSjPWsZOSWuA/viewform?usp=sf_link

  👉ІУ. Домашнє завдання. Повторити п.4-5, с.34-45. "Пригадай головне" с.36 (1-3), с.42 (1-4). №75 (1,2), №76 (1,2). Виконати письмово у зошиті задачі тестового  контролю.

Дистанційне навчання з 15.03.21 по 10.05.21

Алгебра

Урок №11 (20.04.21)

Тема: "Розв'язування систем лінійних рівнянь способом додавання"

👉І. Усно.

1. Повторити п.28, с.200-202.

2. Повторити алгоритм.

Щоб розв’язати систему лінійних рівнянь методом додавання, треба: 

1)  Дібравши «вигідні» множники, перетворити одне чи обидва рівняння системи так, щоб коефіцієнти при одній зі змінних стали протилежними числами; 

2) Додати почленно ліві й праві частини рівнянь, отриманих на першому кроці; 

3) Розв’язати рівняння з однією змінною, отримане на другому кроці; 

4) Підставити знайдене на третьому кроці значення змінної в будь-яке з рівнянь вихідної системи; 

5)  Обчислити значення другої змінної та записати відповідь.

👉ІІ. Письмово.

Приклад:

Завдання 1. Розв'язати систему рівнянь : 2х+у =11 

3х - у=9 {3x−y=9,2x+y=11. }

Розв'язання. 

1. Коефіцієнти при змінній y у є протилежними числами тому додаємо почленно ліві й праві частини рівнянь.

3х - у + 2х + у = 9 + 11

3х + 2х - у + у = 20

5х = 20

х = 20 : 5

х = 4. 

2. Підставимо знайдене значення x у друге рівняння системи і знайдемо y.

2⋅x+y=11 
2⋅4+y=11 
8+y=11 
y=11−8 
y=3  

Відповідь: (4; 3).

👉ІІІ. Домашнє завдання. Повторити п.28, с.200-202. №1047 (2, 3), №1050 (1, 3) 

Дистанційне навчання 14.12.20

Алгебра.

Урок №1 (14.12.20)
Тема: "Тотожності. Одночлен. Многочлен.Самостійна робота"
І. Усно.

Повторити п.10-13, с.65-88.

ІІ. Письмово.

1) Виконайте множення:
а) -3в(а2+6ав+5в2);  (в2 - в у квадраті)
б) (х+5)(у-7);
в) (5m-2n)(3m+n).
2) Розкладіть на множники:
а) 6а2-12ав;
б) -4а4+20а10; (а10 - а у десятому степені)
в) 4а-4в+са-св.
3) Розвяжіть рівняння:
а) 8у2-3у=0;
б) 2х(3х-4)-3х(2х-5)=7.
4) Спростіть вираз:
(х+3)(х-7)-4х(5-2х). 
5) розкладіть на множники та знайдіть значення 3х3+х2-3х-1, якщо а=2 2/3 (дві цілих дві третіх) 
6) Доведіть, що значення виразу: 27 у 7 степені плюс 3 у 18 степені ділиться націло на 7 (дивись зразок: с.79, приклад 5). 
7) Розкладіть на множники: х2+8х+15. (Запишіть  8х у вигляді суми двох доданків (3х+5х) та застосуйте спосіб групування для розкладання многочлена на множники). 

ІІІ. Домашнє завдання. 

Мерзляк А.Г., с.99, "Тематичне оцінювання №3", 1 варіант.

Завдання з дистанційного навчання з 19.10.20 по 23.10.20

Геометрія.

Урок №2. 23.10.20

Тема. Ознаки паралельності прямих.

І. Усно. 

1. Повторити п.7 (урок 1)
2. Вивчити п.8, с.58.
3. Теорема (ознака паралельності прямих)
Якщо при перетині двох прямих січною виконується принаймні одна з умов:
 внутрішні різносторонні кути рівні;
 сума внутрішніх односторонніх кутів дорівнює 
 відповідні кути рівні,
то дані прямі паралельні.
 
Наприклад, якщо ∠3=∠5, то 

 

4. Наслідки 1,2,3.
Ознаки паралельності прямих на площині.
 1. Дві прямі, паралельні третій, паралельні між собою.
 2. Якщо дві прямі на площині перпендикулярні до однієї й тієї самої прямої, вони паралельні.

5. Задача с.60.
6. Відповісти на запитання 1-4 "Пригадайте головне".
7. Виконати: №235,№240, №242.

ІІ. Письмово.

1. Відомо, що дві паралельні прямі перетинає січна. Знайти інші кути.

 

2.№237(1,2), №241(1,3), №243(1,2), №246(1).

ІІІ. Домашнє завдання. 

Вивчити п.8, виконати №239, №244, №247.

Алгебра
Урок №1. 19.10.20.
Тема: "Степінь з натуральним показником"
І.Усно.

1. Вивчити п.5 (с.32-33).
2. Теоретична частина.
Поняття степеня з натуральним показником.

1). Існує короткий запис для множення числа кілька разів самого на себе, наприклад:
 
Під an, де n=2,3,4,5,..., розуміють добуток n однакових множників, кожним з яких є число a.
Вираз   an називають степенем, число a — основою степеня,
число n — показником степеня.
2).
 
 — степінь з натуральним показником;
 — основа степеня;
 — показник степеня.

5⋅5⋅5⋅5⋅5⋅5⋅5=577разів

a⋅a⋅a⋅...⋅a=annразів

3.  Завдання 1.

Використовуючи відповідні терміни, записати у вигляді степеня добуток: 3⋅3⋅3⋅3⋅3.
Розв’язання.
Оскільки дано добуток п’яти однакових множників, кожен з яких дорівнює 3, маємо:

 — степінь;
 — основа степеня;
 — показник степеня.
Завдання 2.
Обчислити: 
a) 
Розв’язання:(−3)4=(−3)⋅(−3)⋅(−3)⋅(−3)=81.
 
 б)
Розв’язання.(411)2=411⋅411=4⋅411⋅11=16121.
в)

 120=1⋅1⋅....⋅1=120раз09=0⋅0⋅....⋅0=09раз.

Завдання 3.
Степенем числа a із показником 1 називають саме це число:  
 01=0(−25)1=−25(117)1=117.

Завдання 4. №152 (с.34)
Завдання 5. Відповісти на запитання 1-6 (с.34).

ІІ. Письмово. 

№153, №155, №162, №164 (непарні).

№162. Розвязання. 
1) ...=64-1=63; 
2) ...=0,3*16=4,8; 
3) ...=0,4*0,4*0,4*0,4*625=16; 
4) ...=(216:200-0,16):0,008=0,92;0,008=920:8=115. 

ІІІ. Домашнє завдання.

п.5. №156, №163, №165.