Блог учителя математики: 8 клас (2)

8 клас (2)

Дистанційне навчання з 17.01.22 по 19.01.22;

з 26.01.22 по 04.02.22

Геометрія

Урок 04.02.22

Тема:"Співвідношення між сторонами і кутами прямокутного трикутника. Розвязування задач"

👉І. Усно.

1.   Як знайти гіпотенузу прямокутного трикутника, коли відомі катет і гострий кут?
2.   Як знайти гострий кут прямокутного трикутника, коли відомі протилежний цьому куту катет і гіпотенуза?
3.   Як знайти гострий кут прямокутного трикутника, коли відомі прилеглий до цього кута катет і гіпотенуза?
4.   У прямокутному трикутнику KMN (рис. 2) відомі катет MN і кут К. Виразіть через них другий катет і гіпотенузу трикутника.

ПОВТОРИТИ:

1) Катет, протилежний до кута а, дорівнює:

✵ добутку гіпотенузи на sin α: а = c sin α

✵ добутку прилеглого катета на tg α: a = b tg α

2) Катет, прилеглий до кута α, дорівнює:

✵ добутку гіпотенузи на cos α: b = c cos α

✵ відношенню протилежного кадета до tg α:

3) Гіпотенуза дорівнює:
✵ відношенню протилежного катета до sin α:

✵ відношенню прилеглого катета до cos α:

👉ІІ. Письмово.
1. У прямокутному трикутнику катет завдовжки 7 см є прилеглим до кута 60°. Знайдіть гіпотенузу трикутника.

Розвязання. = 7 : cos 60 = 7 * 1/2 = 7*2=14 (см).

2. У прямокутному трикутнику гіпотенуза дорівнює 20 см, а синус одного з кутів — 0,6. Знайдіть катети трикутника.

Розвязання. а = c sin α = 20 * 0,6 = 12 (см), b = √(c2 - а2)

=√(400 - 144) = √256 = 16 (см).

3. Визначте невідомі сторони прямокутного трикутника ABC (C = 90°), якщо:
1) АВ = с, A = α; 2) AC = b, B = β; 3) ВС = а, B = β.

Розвязання. 1) b = c cos α; а = c sin α; 2) a = b/ tg β;

с = b/ sinβ; 3) b = а tg β ; с = а / cos β.

4. Знайдіть бічну сторону рівнобедреного трикутника, якщо його основа дорівнює 24 см, а медіана, проведена до бічної сторони, дорівнює 30 см.

Вказівка. Добудуйте трикутник до паралелограма та скористайтеся правилом: "сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін". Одна сторона паралелограма - бічна сторона рівнобедреного трикутника, друга його сторона - основа рівнобедреного трикутника.

Відповідь: √17.

5. У рівнобічній трапеції діагональ дорівнює 17 см, а висота трапеції — 8 см. Знайдіть середню лінію трапеції.

Розвязання. Розглянемо прямокутний трикутник з гіпотенузою 17 см і катетом 8 см. Тоді другий катет √(17-8)(17+8)= √9 * √25 = 3 * 5 = 15 (см) - є середня лінія трапеції.

👉ІІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSciOMtaLJRGmOfi6D__mVfgjAU0xKssfpeAvI1HTz_uYO5zVg/viewform?usp=sf_link

👉ІІІ. Домашнє завдання.

Вивчити п.17, №825,№827, №829, №835.

Алгебра

Урок 02.02.22

Тема:"Арифметичний квадратний корінь з добутку, дробу і степеня"

👉І. Усно.

1. Обчисліть: ; ; ; ·; ;

; ; ; ·.
2. Спростіть: ; ; при b ≥ 0;

при у ≤ 0.

👉ІІ. Письмово.

1. Знаходження значень виразів, що містять корінь з парного степеня дійсного числа.
1) Знайдіть значення виразу: а) ; б) ; в) .
Перевір себе:

а) 25, б) 27, в) 1,44.
2) Знайдіть значення виразу: а) ; б) ; в) .
Перевір себе:

а) ...=(28-22)(28+22)=6*50=350, б)...=2,5+2,5=5 ,

в)...=1,8(1,8-1)= 1,8*0,8=1,44.
3) Обчисліть значення виразу (якщо воно має зміст):

а) =12; б) =-10; в) - не має змісту; г) =-11; д) - не має змісту; є) =-25.
4) Обчисліть: а) ; б) ; в) ; г) ; д) ; є) ; ж) ; з) .
2. Знаходження значень виразів, що мають вигляд кореня з добутку або частки чисел, які потребують попереднього розкладання на прості множники.

Знайдіть значення виразу:

а) =√92162=34*2=24; б) ; в) ;

г) ; д) ; є) .
3. Спрощення виразів, які мають вигляд квадратного кореня з квадрата або парного степеня раціонального виразу (або можуть бути подані в такому вигляді після виконання тотожних перетворень).

Спростіть вираз: а) , де у ≥ 0; б) ;

в) = Іх3І = -х3, де х < 0; г) ; д) ;

є) , де t < 0.

👉ІІІ. Домашнє завдання. Повторити п.п.15, с.115-118. Розвязати №484, №486, №489, №490.

Геометрія

Онлайн - урок 01.02.22

Тема:"Співвідношення між сторонами і кутами прямокутного трикутника"

👉І. Усно.

1. Вивчити п.17, с.122-123.

2. Таблиця 26, задача (с.123).

3. "Пригадайте головне" 1-3, с.124.

4. №810-№813.

👉ІІ. Письмово.

№814, №817, №819, №821.

👉ІІІ. Домашнє завдання. Вивчити п.17, №815,№818, №820, №822.

Алгебра

Онлайн - урок 31.01.22

Тема:"Арифметичний квадратний корінь з добутку, дробу і степеня"

👉І. Усно.

1.   Чи правильна рівність: ; ; ; ; ; .
2.   Знайдіть значення виразів: ; ;
; ; ;
3. Вставте пропущений вираз: а ≥ 0; b > 0
; ; ; .
4.   Обчисліть: |-5|; |-2,42|; ; |0|.

5. Спростіть: |-а6|; |х2|; |-у2 – 1|; |х – 1|.

👉ІІ. Вивчення нового матеріалу.

1. Підручник: вивчити п.15, с.115-118. Приклад 4, приклад 5.

2. Письмово №475 (1,4,7), №477 (1,3,5,7), №481(непарні), №483 (1,3,5) (дивись приклад 4, с.117), №487 (1,2,8), №491 (1) (дивись приклад 5, с.118).

Зразок.

№481 (2,3,6,8).

2) √(1832)=√(92162)=√9√16√4=342=24;

3) √(3,614,4)=√(360,11440,1)=√36√144√0,01=6120,1=7,2;

6) √(4,572)=√(90,5362)=√9√36√1=361=18;

8) √(8045)=√(16595)=√16√9√25=4360.

👉ІІІ. Домашнє завдання. Вивчити п.15, приклади 1-5, №476, №481 (непарні), №488 (2,3), №492 (1).

Геометрія

Онлайн - урок 28.01.22

Тема:"Значення тригонометричних функцій кутів 30, 45, 60 градусів"

👉Домашнє завдання. Вивчити п.18, с.127-130. Відповісти на запитання "Пригадайте головне" 1-4, с.130. Розвязати №857, №859.

Урок 26.01.22

Тема: "Властивості арифметичного квадратноо кореня"

👉І. Усно.

1. Яка з рівностей є правильною?
а) ; б) ; в) ; г)
2.   Обчисліть значення виразу: ; ; ; .
3.   Обчисліть: ; ; .
4. Обчисліть: а) ; б) ; в) ; г) ; д) ; є) ; ж) 2.

👉ІІ. Вивчення нового матеріалу.

1. Підручник п.15, с.115-118. Теореми 15.1-15.4.

1) Виписати формули. Дивись форзац 2 підручника. "Властивості арифметичного квадратного кореня".

2) Конспект прикладів 1, 2, 3 (с.116-117).

2. Натисніть на посилання. Продивіться відео.

https://youtu.be/m7loxlMqkqk

👉ІІ. Домашнє завдання.

Вивчити п.15, с.115-118, №474, №478, №482.

Геометрія.

Урок 20.01.22

Тема:"Теорема Піфагора. Перпендикуляр і похила. Середні пропорційні у прямокутному трикутнику".

👉І. Усно.

1. Робота з підручником.

1) Повторити п. 15, 17.

2) Відповісти на запитання ☝"Пригадайте головне"1-4 (с.113), 1-3 (с.124).

👉ІІ. Письмово. Розвяжіть тестові задачі.

👉ІІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSe1uI5FNqJQnZQYDNvX3ssG0mtIBsKJ70zVqIqeMoedVjqUfQ/viewform?usp=sf_link

Алгебра.

Урок 19.01.22

Тема:"Числові множини. Раціональні числа".

👉І. Усно.

1. Розвяжіть рівняння: х2-21=0.

а) 21; б)士√21; в) коренів немає; г) 0.

2. Знайдіть корінь рівняння: 3 у2 - 4,8 = 0.

а) 0,4; б) √1,6; в) √土1,6; г) коренів немає.

3. Виберіть правильне твердження. Рівняння .

А
Б
В
Г
не має жодного кореня
має один раціональний корінь
мас два ірраціональні корені
має один ірраціональний корінь

☝ІІ. Вивчення нового матеріалу.

1. Робота з підручником.

1) Вивчити п. 14 с.105-110.

2) Відповісти на запитання 1-10 с.110.

2. 👉Написати конспект.

3. Виконання усних вправ.
1) Чи правда, що:

а) будь-яке ціле число є дійсним;
б) будь-яке ірраціональне число є дійсним;
в) будь-яке дійсне число є раціональним?

2) Укажіть правильне твердження:
а) n — число дійсне;
б) 2,222... — число раціональне;
в) 2,212211222111... — число раціональне;
г) - 2 — число дійсне.

👉ІІІ. Письмово. Підручник с.110-11, №444, №453.

👉ІУ. Домашнє завдання.

Вивчити п.14 с.105-110. Виконати №445, №449, №454, №456.

Геометрія.

Урок 18.01.22

Тема:"Перпендикуляр і похила та їх властивості.

👉І. Усно.

Розминка. Інтерактивна технологія «Мікрофон»

1. Який трикутник називають прямокутним?
2. Чому дорівнює сума гострих кутів прямокутного трикутника?
3. Як називають найдовшу сторону прямокутного трикутника?
4. Чи може в прямокутному трикутнику бути два прямих кути?
5. Чи може в прямокутному трикутнику бути два рівних катети?
6. Чому дорівнюють кути такого трикутника?
7. Якщо сторони трикутника дорівнюють 6 см, 8 см, 10 см, то кут, протилежний стороні 10 см, дорівнює... (90°).
8. Сформулюйте теорему Піфагора.
9. Якщо в прямокутному трикутнику катет, протилежний куту 45°, дорівнює 7 см, то другий катет дорівнює... (7 см).
10. Якщо гіпотенуза прямокутного трикутника дорівнює 8 см, то катет, прилеглий до кута 60°, дорівнює... (4 см).

👉ІІ. Розв'язування задач за готовими рисунками

Метод «Мозковий штурм»
Знайдіть х. Задача 3. Знайти сторону ромба АВСД.
1
2
3
4

АС=6, BD=8

Р=4а

👉IІІ. СПРИЙНЯТТЯ Й УСВІДОМЛЕННЯ НОВОГО

Робота за підручником.
Прочитайте самостійно текст § 15 (2), с.110-112 підручника і дайте відповіді на запитання.
1. Що таке перпендикуляр, похила?
2. Поясніть, що таке проекція похилої.
3. Скільки різних похилих можна провести з поданої точки до прямої? А скільки перпендикулярів?

👉ІV. ПЕРВИННЕ ЗАКРІПЛЕННЯ НОВИХ ЗНАНЬ
Розв'язування задач
Задача 1. З однієї точки до прямої проведено дві рівні похилі. Відстань мпк їх основами становить 12 см. Визначте проекції похилих на подану пряму.
Відповідь. 6 см, 6 см.
Задача 2. Бічна сторона рівнобедреного трикутника більша за основу і дорівнює 13 см, а проведена до неї висота — 5 см. Знайдіть довжину більшого з відрізків, на які висота ділить бічну сторону трикутника.
Розв’язання
Нехай ΔАВС – поданий рівнобедрений трикутник, У якому АВ=ВС=13 см. Оскільки СК – висота, проведена до бічної сторони, а BC>AC, то BK>AK, тобто ВК – більший з відрізків, на які висота ділить бічну сторону трикутника.
Із прямокутного ΔВКС (),
см.
Відповідь. 12 см.
Задача 3. Основи рівнобічної трапеції дорівнюють 7 см і 15 см, гострий кут — 60°. Знайдіть периметр трапеції.

Розв’язання
Нехай АВСD – подана рівнобічна трапеція (ВС||AD), у якої ВС=7 см, AD=15 см, .
Проведемо висоту ВК.
(см).
У прямокутному трикутнику АКВ ()
.
як катет, що лежить проти кута 30°.
АВ=8 см.
Р=2АВ+ВС+AD, Р=16+7+15=38 (см).
Відповідь. 38 см.

👉У. Домашнє завдання.

Вивчити п. 15 (2), №744, №763 Застосуйте теорему Піфагора для прямокутного трикутника.

Алгебра.

Урок 17.01.22

Тема:"Квадратний корінь. Арифметичний квадратний корінь"

👉І. Усно.

1. Знайдіть квадрати чисел: 10; -8; 2/7; 0,9.

Відповідь. 100; 64; 4/49, 0,81.
2. Знайдіть значення виразів при х = -5:
1) х2; 2) (х – 2)2; 3) (х + 1)2; ; 4) |х|; 5) |х – 5|;
6) 2|х| – 3; 7) |х + 5|, 8) .
Відповідь. 1) 25; 2) 49; 3) 16; 4) 5; 5) 10; 6) 7; 7)0; 5/2.

👉ІІ. Вивчення нового матеріалу.

1. Написати конспект.

1) Рівняння х2 = а
Квадратним коренем із числа a називається число, квадрат якого дорівнює a.
Арифметичним квадратним коренем із числа a називається невід’ємне число, квадрат якого дорівнює a.

Читаємо — «корінь квадратний з a».

Знаком арифметичного квадратного кореня служе радикал .
Число a називається підкореневим виразом ().
Не існує кореня квадратного з від’ємного числа.
Якщо корінь квадратний із числа a має смисл, то квадрат цього кореня дорівнює самому числу a:.
Корінь квадратний із нуля дорівнює нулю: .

2) Запамятай.

а) якщо число х є коренем рівняння х2 = а, то х — квадратний корінь з числа а:

б) якщо число х ≥ 0 є коренем рівняння х2 = а, то х — арифметичний квадратний корінь х числа а.

Записують: .

Запам'ятай! Запис означає, що а ≥ 0, х ≥ 0 і х2 = а.

2. Виконання письмових вправ.

1)   Знайдіть арифметичний квадратний корінь із чисел: а) 81; б) 0,09; в) 0.
Розвязання.а)  = 9; б)  = 0,3; в) .
2)   Чи має зміст вираз: а) ; б) ; в) ?
Відповідь. а) 16; б) не має змісту, бо -16く0, в) 4, бо -2*(-8)=16.

3)   Розв'язування рівнянь виду
(або зводиться до виду)  = а.
4) Чи існує значення змінної х, при якому:
а)  = 0,1; б)  = – 10; в)  + 1 = 0; г)  – 3 = 0?

Відповідь. а) х=0,01; б) не існує, бо -10 відємне число,

в) не існує бо √х ≥ 0; г) 9.

5) Знайдіть значення змінної х, при якому правильна рівність: а) ; б) ; в) .

Розвязання. Піднесіть обидві частини рівняння до квадрату.

а) 3+5х=49; 5х=49-3; 5х=46; х=46/5.
б) 10х-14=121; 10х=135; х=13,5.
в) 1/3х-1/2=0; 1/3х=1/2; х=1/2:1/3; х=1/2*3/1; х=3/2.

6) Перевір себе. В якому з випадків правильно виконано дію?

а) ; б) ; в) ; г) ; д) .

👉ІІІ. Домашнє завдання.

Вивчити п.12 (с.88-91), приклади 1, 5. Вивчити конспект. Письмово №384 (див. форзац 3), №388 (користуйся формулою: (для a ≥ 0)..), №394, №402 (4, 4).

Геометрія

Урок 14.01.22

Тема:"Середні пропорційні у прямокутному трикутнику".

І. Усно.

Повторити п.15 (1), с.110-111, відповісти на запитання 1-2 "Пригадайте головне" с.113.

👉ІІ. Вивчення нового матеріалу.

Вивчити п.14 (с.99-101).

1. Що таке середнє пропорційне між двома відрізками?

Відрізок 𝑥 називають середнім пропорційним між відрізками 𝑎 𝑖 𝑏, якщо:

𝒂 𝒙

=
х b
Чи можна записати цю рівність інакше? Пригадайте основну властивість пропорції: х2=аb.

2. Чи можна встановити співвідношення між довжинами відрізків у трикутнику?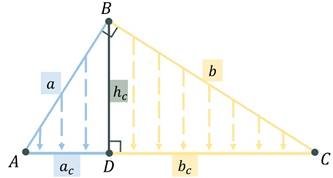
У прямокутному трикутнику, висота (ℎ𝑐) проведена до гіпотенузи (𝑐) ділить її на відрізки 𝐴𝐷 𝑖 𝐷𝐶 (𝑎𝑐 𝑖 𝑏𝑐). Ці відрізки називаються проекціями катетів (𝑎 𝑖 𝑏) на гіпотенузу.

Співвідношення між довжинами деяких відрізківу у трикутнику і колі називаються метричними.

Теорема (метричні співвідношення в прямокутному трикутнику).

1) Висота, проведена до гіпотенузи є середнім пропорційним між проекціями катетів на гіпотенузу.

Запишіть формули: ВД2=АД*ДС (див. рис.)

2) Катет є середнім пропорційним між гіпотенузою і його проекцією на гіпотенузу.

Запишіть формули: АВ2=АСАД; ВС2=АСДС (див. рис.)

3. Наслідок. Задача (конспект).

👉ІІІ. Усно. №689-№691, №693.

👉ІУ. Письмово. №694(1), №696 , №698.

👉У. Домашнє завдання. Вивчити п.14 (с.99-101. Відповісти на запитання 1-4 "Пригадайте головне (с.101). Виконайте №695, №697, №699.

Алгебра

Урок №2 (12.01.22)

Тема: "Функція у=х2, її властивості і графік.

👉І. Перевірка домашнього завдання.

№351

1) Якщо х=-8, то у=(-8)2=64, 64=64. Графік функції у=х2 проходить через точку А(-8;64).

2) Якщо х=-9, то у=(-9)2=81, 81≠-81 (не проходить).

3) Якщо х=0,5, то у=(0,5)2 =0,25, 0,25≠2,5 (не проходить).

4) Якщо х=0,1, то у=(0,1)2=0,01, 0,01=0,01 (проходить).

№358

1) f(х)=2х+3, якщо х≤-1.

Якщо х=-4, то f(-4)=2*(-4)+3=-8+3=-5.

Якщо х=-1, то f(-1)=2*(-1)+3=1.

2) f(х)=х2, якщо -1≤х＜2.

Якщо х=-0,3, то f(-0,3)=(-0,3)2=0,09.

Якщо х=1,9, то f(1,9)=(1,9)2=3,61.

3) f(х)=4, якщо х≥2.

Якщо х=2, то f(2)=4.

Якщо х=3, то f(3)=4.

👉ІІ. Повторити п.11 (с.83-85), відповісти на запитання 1-5 (с.85).

👉Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSfdRgKBF7tjDI7QWxRZFYQp7WCg9QbwG8gVVO9YZTDSiFprmQ/viewform?usp=sf_link

👉ІІІ. Домашнє завдання.

Повторити п.11 (с.83-85), відповісти на запитання 1-5 (с.85), №353(3), №373, №375.

Геометрія.

Урок 11.01.22

Тема: "Теорема Піфагора"

👉І. Теорія.

Одна з найвідоміших геометричних теорем — теорема Піфагора, знаменитого давньогрецького філософа і математика.
В історії математики знаходимо твердження, що цю теорему знали за багато років до Піфагора, наприклад, стародавні єгиптяни знали про те, що трикутник зі сторонами _3, 4
і 5
є прямокутним.

У наш час теорема звучить так (маючи на увазі не тільки площі, але і довжини сторін прямокутного трикутника):

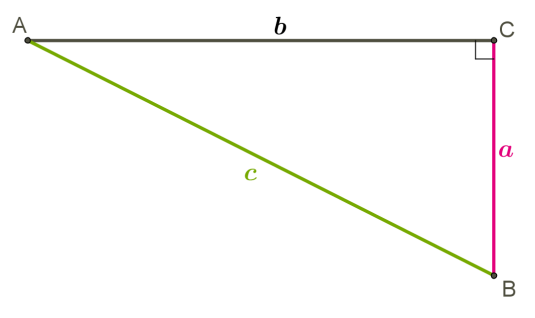У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів c2=a2+b2.

Якщо знаходимо довжину гіпотенузи c, тоді виконуємо додавання квадратів довжин катетів a і b і визначаємо квадратний корінь:

c2=a2+b2c=a2+b2−−−−−−√
Якщо знаходимо довжину одного катета, тоді виконуємо віднімання довжини квадрата іншого катета з квадрата довжини гіпотенузи і визначаємо квадратний корінь:

a2=c2−b2a=c2−b2−−−−−−√

👉ІІ Письмово.

1. Чи є трикутник зі сторонами 6см, 7см і 9см прямокутним?
Обираємо більшу сторону і перевіряємо, чи виконується теорема Піфагора: 36+49≠81, отже, цей трикутник не прямокутний.

2. Чи є трикутник зі сторонами 5см, 12см і 13см прямокутним?
Обираємо більшу сторону і перевіряємо, чи виконується теорема Піфагора: 25+144=169, отже, цей трикутник прямокутний.
3. Щоб не витрачати багато часу на розв'язання, корисно запам'ятати найбільш використовувані числа Піфагора:
катет, катет, гіпотенуза
3; 4; 5
6; 8; 10
12; 16; 20
5; 12; 13. (Перевірте письмово).

4. Катети прямокутного трикутника дорівнюють 10 см та 24 см. Знайти гіпотенузу.

5. Катет прямокутного трикутника дорівнює 6 см, а гіпотенуза 10 см. Знайти другий катет та площу прямокутного трикутника (S= 1/2 ab, а, b- катети прямокутного трикутника).

👉ІІІ. Домашнє завдання. Вивчити п.15, с.110-111 (п.1). Задача (с.111), конспект. Виконати №731(1), №732(1), №736.

Алгебра.

Урок 10.01.22

Тема:"Функція у=х2, її властивості і графік.

👉І. Усно.

1. Знайдіть область визначення функції:

а) 1/(х-5); б)5/(х2-9) ; в) 1/ІхІ .

2.   Функцію задано формулою у = 16/х.
а) Якого значення набуває функція, якщо аргумент дорівнює 4?
б) При якому значенні аргументу значення функції дорівнює 2?
3.   Чи проходить графік функції у = 1/х через точки: а) А(-1; 1); б) В(1/2;2); в) С; г) D?
4.   Визначте знак виразу: а) (-3)10; б) (-x – 1)2 ; в) -x2 – 1.
5.  Як називається графік функції у=к/х при k ≠ 0? Опишіть властивості функції.
6. Опишіть вид графіка функції у=к/х (при k ≠ 0) при k > 0; k < 0.

👉ІІ. Засвоєння нових знань.

1. Вивчити п.11, с.83-85.

1) Область визначення функції у=х2 (усі числа)

2) Область значень функції у=х2 (усі невід'ємні числа)

3) Побудова графіка функції у=х2 (парабола)

4) Нулі функції (значення аргументу, при якому значення функції дорівнює 0) х=0

5) Властивості графіка. Якщо точка А(Хо;Уо) належить параболі у=х2, то точка В(-Хо;Уо)також належить цій параболі)

6) Приклад. Розвяжіть графічно рівняння: х2=2х+3 (див. рис.)

👉ІІІ. Письмово.

1. Користуючись графіком функції у = х2 (див. рис.), знайдіть:

1) значення функції, яким відповідають такі значення аргументу: -1; 1; 2; 3.

2) значення аргументу, яким відповідають такі значення функції: 0; 2; 4; 9.

2. №350, №353(1) (с.85).

👉ІУ. Домашнє завдання.

Вивчити п.11 (с.83-85). Відповісти на запитання 1-3 (с.85).

Виконати №351, №354 (1), №358.

Дистанційне навчання з 13.10.21 по 24.11.21

Алгебра

Урок 24.11.21

Тема: "Множення і ділення раціональних дробів. Тест-контроль"

👉І. Усно.

1. Підручник. Повторити п.5-7 с.32-50,

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSfaOloSVYeUcgBW0HM1os-k93-IuraE9c-X67OUW53RiKr-0Q/viewform?usp=sf_link

👉ІІІ. Домашнє завдання. Повторити п.5-7 с.32-50. Письмово розвязати тестові завдання.

Геометрія

Урок 23.11.21

Тема: "Розвязування задач"

👉І. Усно.

1. Підручник.

1) Повторити п.6-9.

2) Відповісти на "Контрольні запитання" 1-12, с.66.

3) Тестові завдання №2, с.67.

👉ІІ. Письмово (розвязати задачі тестового завдання).

Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSf10nZ3xtO2Ag1qm0wtGo-afxj5nD23yk4Bcom0YQA-Vp3hXQ/viewform?usp=sf_link

👉ІІІ. Домашнє завдання. Повторити п.6-9. Відповісти на "Контрольні запитання" 1-12, с.66. Письмово №440, №446, №406, №356.

Алгебра

Урок 22.11.21

Тема: "Розвязування задач, складаючи дробово-раціональне рівняння"

👉І. Усно.

Обери правильну відповідь.

1) Рівняння, ліва і права частина яких є раціональними виразами, називають…
А) дробовими;
Б) раціональними;
В) цілими раціональними;
Г) лінійними.
2) Щоб дріб дорівнював нулю, необхідно, щоб …
А) знаменник і чисельник дорівнювали нулю;
Б) знаменник дорівнював нулю, а чисельник не дорівнював нулю;
В) чисельник і знаменник не дорівнювали нулю;
Г) чисельник дорівнював нулю, а знаменник не дорівнював нулю.
3) При яких значеннях змінної дріб x/(x-6 ) дорівнює нулю?
4) При яких значеннях змінної дріб 6/(x-6 ) дорівнює нулю?
👉ІІ. Вивчення нового матеріалу.

1. Підручник п.7. Приклад 4.

2. Конспект.

Задача 1. Теплохід пройшов за течією річки 150 км і повернувся назад, витративши на весь шлях 5,5 години. Знайдіть швидкість течії річки, якщо швидкість теплохода в стоячій воді 55 км/год.
Розв’язання

Рух Швидкість (км/год) Час (год) Відстань (км)

За течією 55+х 150/(55+х) 150

Проти течії 55-х 150/(55-х) 150

Нехай швидкість течії річки х км/год. Тоді за течією теплохід рухався зі швидкістю (55+х) км/год і пройшов 150 км. Проти течії теплохід рухався зі швидкістю ( 55-х) км/год і пройшов 150 км. За умовою задачі, на весь шлях він витратив 5,5 год. Складемо й розв’яжемо рівняння.

150/(55+х) + 150/ (55-х) = 5,5; 5,5=55/10=11/2.

150/(55+х) + 150/(55-х) = 11/2, помножимо на 2

300/(55+х)+300(55-х)=11, зведемо до спільного знаменника

300(55-х) + 300(х+55)-11(3025-х2) = 0,

при умові (х+55)(х-55)≠0, х≠ 土55.

Розкриємо дужки і зведемо подібні: х2=25, х=5; х=-5.

Розв’язок -5 не задовольняє умову задачі: швидкість – число додатне.
Відповідь: швидкість течії 5 км/год.

Задача 2. Чисельник звичайного дробу на 7 менший від його знаменника. Якщо чисельник зменшити на 1, а знаменник збільшити на 4, то дріб зменшиться на 1/6. Знайдіть даний дріб.
Розв’язання: 1. Вводимо змінну: х – чисельник початкового дробу.
2. Заповнюємо базову таблицю:
Початковий Змінений
Числельник х х-1
Знаменник х+7 х+7+4=х+11
Дріб х/(х+7) (х-1)/(х+11), менший на 1/6
3. Звертаємо увагу що для рівняння ми використовуємо 2 останні стовпці таблиці.
Складаємо рівняння: х/(х+7) - (х-1)/(х+11) = 1/6 .

4. Розв’язуємо рівняння.
5. Записуємо відповідь.

👉ІІІ. Домашнє завдання. Вивчити п.7 (приклад 4), с.46-50, №214, №216.

Урок 19.11.21

Тема: "Середня лінія трапеції"

👉І. Математичний диктант.

1.   Дві сторони трикутника сполучили відрізком, не паралельним до третьої сторони. Чи є цей відрізок середньою лінією трикутника?
2.   У трикутнику ABC сторона АВ дорівнює 6 м Чому дорівнює середня лінія трикутника ABC, яка паралельна стороні АВ?
3.   Точки М, Р і О — середини сторін трикутника ABC. Знайдіть периметр трикутника ABC, якщо сторони трикутника МРО дорівнюють 3 см, 4 см і 5 см.
4.   Кінці відрізка АВ лежать на двох сторонах трикутника, а довжина цього відрізка дорівнює половині третьої сторони. Чи обов'язково АВ є середньою лінією трикутника?

👉ІІ. вивчення нового матеріалу.

1. Означення середньої лінії трапеції.

2. Властивість середньої лінії трапеції.

Конспект
Середня лінія трапеції
Означення. Середньою лінією трапеції називається відрізок, що сполучає середини бічних сторін трапеції.
Властивості
1. Якщо MN — середня лінія трапеції ABCD (BC || AD), то: MN || AD (BC) і MN = 1/2 (AD+ ВС).
2*. Середня лінія трапеції ділить навпіл будь-який відрізок, кінці якого лежать на основах трапеції
3. Якщо ABCD - трапеція (BC\\AD), 0 — точка перетину діагоналей, MN — середня лінія, то Р і Q — середини діагоналей АС і BD:
QN=1/2BC,PQ=1/2(AD-BC)

3. Підручник. Вивчити п.7 (2), с.44-47.

4. Усно. Знайдіть х (№332, с.49).

5. Виконання письмових вправ

1. Знайдіть:

а) середню лінію трапеції з основами 8 см і 12 см;

б) основи трапеції, діагональ якої ділить середню лінію на

відрізки завдовжки 3 см і 4 см.

2. Основи трапеції 8 см і 12 см. Знайдіть відрізки середньої лінії, які містяться між діагоналями трапеції.

3. Середня лінія трапеції у 3 рази більша за меншу основу і на 8 см менша за більшу основу. Знайдіть основи трапеції.

👉ІІІ. Домашнє завдання. Вивчити п.7, с.44-47. Письмово №325, №332.

Комментариев нет:

Отправить комментарий

Подписаться на: Сообщения (Atom)