Блог учителя математики: 8 клас

Дистанційне навчання з 21.03.22.

Алгебра

Урок 01.06.22

Тема. "Підсумкова контрольна робота"

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSdvPYG9sR9tDCx-iJP6DNyhPDWVKxWXCk-yNLCiDT5Qe-75Wg/viewform?usp=sf_link

Тестові завдання виконати письмово у зошиті. Фото контрольної роботи надіслати в особисті повідомлення у вайбер або на електронну адресу (для оцінки достатнього та високого рівня)

Геометрія

Урок 31.05.22

Тема. "Підсумкова контрольна робота"

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSeZ0_ki4bXiODYjPgoO9g2aB2s4zSjTKgh_VlLzNrbARZPDDA/viewform?usp=sf_link

(Тестові завдання виконати письмово у зошиті. Фото контрольної роботи надіслати в особисті повідомлення у вайбер або на електронну адресу)

Алгебра

Урок 25.05.22

Тема. "Повторення. "Степінь з цілим показником. Квадратні корені. Квадратні рівняння."

👉І. Усно.

👉ІІІ. Домашнє завдання.

Повторити п.8, с.53; п.9, с.61; п.12, с.88; п.15, с.115; п.16, с.122; п.18, с.141; п.19, с.148. Письмово виконати тестові завдання.

Геометрія

Урок 27.05.22

Тема. "Повторення. Підготовка до річної контрольної роботи"

👉І. Усно.

Повторення вивченого. Таблиці с.179-183.

1.   Сторони прямокутника дорівнюють 3 см і 4 см. Чому дорівнює радіус кола, описаного навколо цього прямокутника?
2. Продовжіть речення:
а) Сума двох гострих кутів прямокутного трикутника дорівнює ... ? (Відповідь. 90°).
б) Якщо катет прямокутного трикутника дорівнює половині гіпотенузи, то протилежний йому кут дорівнює... ? (Відповідь.  30°)
3.   Закінчіть речення: «Якщо в паралелограмі немає жодного гострого кута, то він є...». Поясніть.
4.   Скільки достатньо знати сторін паралелограма, щоб можна було знайти його периметр? Скільки достатньо знати кутів паралелограма, щоб можна було обчислити всі інші його кути?
5. Якщо діагональ паралелограма ділить його кут навпіл, то кут ж діагоналями дорівнює... градусів, тому що...
6.   На рисунку в прямокутному трикутнику ABC B = 90°, A α.
а) Виразіть cos α;
б) виразіть гіпотенузу АС через катет ВС і тригонометричну функцію кута α;
в) виразіть   sin C    через   тригонометричну функцію кута α.

👉ІІ. Письмово.
1.   За даними рис. 1 знайдіть tg α.

2.   На рис. 2 ABCD — прямокутник. Знайдіть х і у.

3.   Знайдіть висоту й бічну сторону рівнобедреної трапеції з основами 2 і 8 та гострим кутом α.
4.   У рівнобедреній трапеції кут при основі дорівнює 135°, менша основа і бічна сторона — відповідно 8 і 10. Знайдіть середню лінію трапеції.
5.   Знайдіть сторону ромба, якщо його діагоналі дорівнюють 8 см і 6 см.
6.   Знайдіть сторону квадрата, рівновеликого прямокутнику зі сторонами 4 см і 9 см.
7.   Сторони паралелограма дорівнюють 9 см і 6 см, а гострий кут — 30°. Знайдіть висоту цього паралелограма, яка проведена до сторони довжиною 9 см.
9.   Один із кутів рівнобедреного трикутника дорівнює 92°. Знайдіть величини всіх інших кутів.
10.   Периметр рівнобедреного трикутника дорівнює 26 см, а його основа — 10 см. Знайдіть бічну сторону трикутника.
8. Визначте довжину кола, якщо площа його круга дорівнює 48π см2.
11. Знайдіть гіпотенузу прямокутного трикутниказ катетами 3 см та 6 см.
12. Знайдіть площу прямокутника , сторони якого 5 см та 10 см.
13. Знайдіть площу прямокутного трикутника з гіпотенузою 13 см та катетом 5 см.
14. У прямокутній трапеції більша бічна сторона 10 см. Знайти площу трапеції, якщо її основи 5 см та 11 см.

Алгебра

Урок 25.05.22

Тема. "Повторення. Властивості та графіки функцій у=k/х; у=х2; у= √х"

👉І. Усно.

1. Повторити п.10, с.69; п.11, с.83; п.17, с.132. Контрольні запитання 1-8, с.73. Таблиця с.72. Контрольні запитання 1-5, с.85. Таблиця с.85. Контрольні запитання 1-7, с.135. Таблиця с.134.

2. Натисніть на посилання. Продивіться відео.

https://youtu.be/uIRqu1PnbOg

3. Логічна вправа:

Який запис пропущено?
Раціональний дріб
Квадрат числа
у = х2
Квадратний корінь
?

4. Запитання.

Який із графіків, зображених на рисунку, є графіком
функції y = x2

👉ІІ. Письмово.

1. Не виконуючи побудови графіка функції у = 5/х, визначте, які з даних точок належать графіку цієї функції:
варіанти відповідей

А(- 1; 5)

В(- 5; -1)

С(2,5; -2)

D(- 2; -2,5)

2. Знайти значення аргументу функції y = x2 - 5, якщо значення функції дорівнює 4.

3. Чи належить графіку функції y = √x точка А(16; 4).

4. Графік функції y =k /x проходить через точку (3; -2). Чи проходить цей графік через точку ( -4; 2) ?

5. Розв'яжіть графічно рівняння x2 = 2x. Вкажіть їх.

Геометрія

Урок 24.05.22

Тема. "Повторення. Многокутники та їх площі"

👉І. Усно.

1. Повторити п.20-24, с.146-178. Контрольні запитання 1-8, с.178. Таблиця с.183.

👉ІІ. Письмово.

1. Площа паралелограма.

Висота паралелограма - перпендикуляр, проведений з будь-якої точки сторони паралелограма до прямої, що містить протилежну паралельну сторону.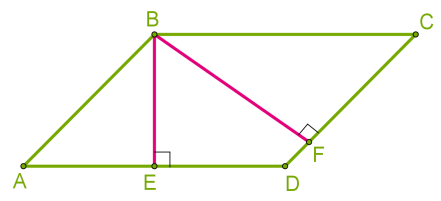
Оскільки сторони ромба однакові, тоді висоти ромба також однакові BE = BF.
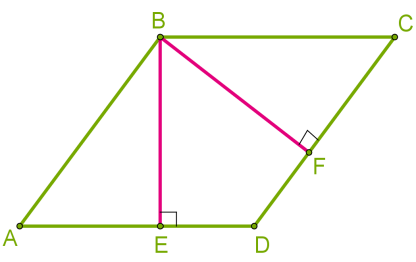2. Площа довільного паралелограма.

Площа паралелограма дорівнює добутку висоти і сторони, до якої проведена висота.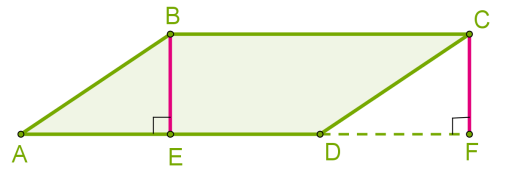
Sпар. = a⋅h.

3. Площа ромба.

Діагоналі ромба в точці перетину діляться навпіл, вони перпендикулярні і ділять ромб на чотири рівних прямокутних трикутника.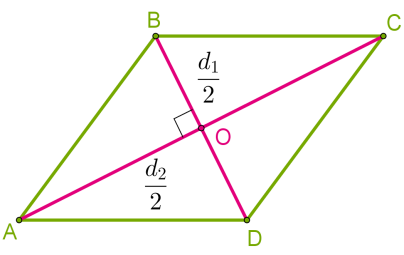
Sромба = ½d1⋅d2.

4. Оскільки діагоналі квадрата рівні, тоді для визначення площі квадрата у формулі достатньо довжини однієї діагоналі:

Sквадрата = ½d2.

5. Площа довільного трикутника.

Оскільки діагональ паралелограма ділить його на два рівних трикутника, тоді площа трикутника дорівнює половині площі паралелограма.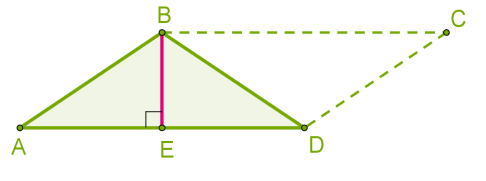
Sтрик = ½a·hа, де h — висота (на малюнку — BE), проведена до сторони a (на малюнку — AD).

6. Для визначення площі трикутника зручно іноді використовувати формулу Герона, якщо відомі довжини всіх трьох сторін трикутника.

SΔ = √p(p−a)(p−b)(p−c), де p = ½(a+b+с) — формула Герона, де a, b, c — сторони трикутника, p — півпериметр трикутника.

7. Площа прямокутного трикутника.

Оскільки катети прямокутного трикутника взаємно перпендикулярні, тоді один катет може бути висотою, а інший катет — стороною, до якої проведена висота.

Отримуємо формулу: S = ½ a⋅b, де a і b — катети.

8. Площа трапеції.

Трапеція має одну пару паралельних сторін, отже, має одну висоту — перпендикуляр, проведений між паралельними сторонами. Найчастіше висоту трапеції проводять з вершин або через точку перетину діагоналей.

Sтрап. = ½ (а + b)·h, де a і b - основи трапеції,h - її висота.

9. Скласти конспект матеріалу. Виконати вправу № 1188 (с.177).

👉ІІІ. Домашнє завдання.

Повторити п. 20 - 24.Тестові завдання №1 (1-5), с.178

Алгебра

Урок 23.05.22

Тема. "Повторення. Тотожні перетворення раціональних виразів"

👉І. Усно.

1. Яка послідовність дій у виразі ?
2. Прокоментуйте виконання дій у виразі .
1) ; 2) ; 3) .
Відповідь. .

👉ІІ. Письмово.

Конспект
1.
Раціональні вирази.

Раціональні рівняння

Цілі вирази

Дробові ви рази

Цілі рівняння
= 2
Дробові рівняння = 2

2. Дробово-раціональне рівняння.

ОДЗ: значення змінної, при яких існують вирази в обох частинах рівняння.

3. Алгоритм розв'язання рівнянь виду = 0 (А і В — многочлен від однієї змінної).
= 0.
1) В ≠ 0 (знайти ОДЗ рівняння):
2) А = 0 (знайти, при яких значеннях змінної чисельник дорівнює нулю);
3) (знайти, які з коренів рівняння А = 0 задовольняють ОДЗ рівняння);
4) Відповідь. (Запишіть у відповідь ці корені)

4. Прокоментуйте (використовуючи алгоритм) розв'язання рівняння .
1) ОДЗ: х ≠ 0 та х + 1 ≠ 0; х ≠ 0 та х ≠ -1;
2) , , ;
3) х – 1 = 0,
х = 1 — входить до ОДЗ.
Відповідь. 1.
5. Розв'яжіть рівняння: а) ; б) ; в) .
6. Розв'яжіть рівняння: а) ; б) ; в) .

Геометрія

Урок 20.05.22

Тема. "Повторення. Теорема Піфагора. Розвязування прямокутних трикутників"

👉І. Усно.

1. Повторити п.15-19, с.110-138.

👉ІІ. Письмово.

В завданнях 1-4 вкажіть правильну відповідь. Кожне завдання оцінюється 1 б.

1. Знайдіть гіпотенузу прямокутного трикутника з катетами 2√ 3 см і 2 см.

А	Б	В	Г
4√ 3см	4 см	8√ 3см	16 см

2. У трикутнику ABC ∠C = 90°, ВС = 18см, tg∠А=2/3. Знайдіть АС.

A	Б	В	Г
27	12	15	4

3. У трикутнику ABC ∠C = 90°, АВ = 26 см, ВС = 24 см. Знайдіть sin∠В.

А	Б	В	Г
2/13	5/12	12/13	5/13

4. Дано прямокутний трикутник ABC із гіпотенузою АВ, відрізок CD — висота даного трикутника. ∠B = 30°, AD = 2 см. Яка довжина відрізка АС?

А	Б	В	Г
2 √ 3см	6 см	3 √ 3см	4 см

Завдання 5-7 розв’яжіть з повним обґрунтуванням.

5. (2 б.) Розв'яжіть прямокутний трикутник з гіпотенузою 6 см і гострим кутом 30°.

6. (3 б.)Із точки до прямої проведені дві похилі, проекції яких на пряму дорівнюють 9 см і 16 см. Знайдіть відстань від точки до прямої, якщо одна з похилих на 5 см більша від іншої.

7. (3 б.) Знайдіть висоту й бічну сторону рівнобічної трапеції з основами 2 і 8 та гострим кутом α.

👉ІІІ. Домашнє завдання.

Контрольні запитання 1-6, с.142. Тестові завдання №1 (1-5), №2 (1-5).

Алгебра

Онлайн урок 18.05.22.

Тема: "Квадратний тричлен. Розв'язування задач за допомогою квадратних рівнянь"

👉І. Усно.

1. Підручник. Повторити п.21-23, с.166-183.

👉ІІ. Письмово.

1. Знайти корені квадратного тричлена: 5х2-х-6.

Розвязання.

Складаємо рівняння: 5х2-х-6=0

Д=(-1)2 - 4*5*(-6)=121.

х1=(1+11):10=1,2

х2=(1-11):10=-1.

2. Квадратний тричлен розкладено на множники

-х2-4х+5=-(х-1)(х+5).

Знайти корені квадратного тричлена.

Розвязання.

Маємо формулу (п.21, с.166):

ах2+bх+с=а(х-х1)(х-х2).

-х2-4х+5=-(х-1)(х+5)

Тоді х1=1; х2=-5.

3. Підручник . Завдання №6 "Перевір себе" у тестовій формі: №7, №9, №10.

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLScd6lmYRb27MJhwwGqby7Cy4aDwsax_9BDht-ZnuOcALGrE7A/viewform?usp=sf_link

Геометрія

Урок 17.05.22

Тема. "Повторення. Подібність трикутників. Розв'язання задач."

👉І. Усно.

1. Повторити п.10-13, с.70-99.

2. Сформулювати умови, за яких ΔABCလ∆A 1 B 1 C 1:

1) за І ознакою ( ∠А= ∠А1, ∠В= ∠В1) за двома рівними кутами;

2) за ІІ ознакою ( ∠А= ∠А1, АВ/А1В1=АС/А1С1) за двома пропорційними сторонами та кутом між ними;

3) за ІІІ ознакою (АВ/А1В1=ВС/В1С1=АС/А1С1) за трьома пропорційними сторонами.

👉ІІ. Письмово.

Задача 1. Сторони одного трикутника дорівнюють

а) 3см, 6см та 7см; б) 5м, 35м і 30м,

а дві сторони подібного йому трикутника

а) 15см та 35см; б) 7м та 6м.

Обчисліть довжину третьої сторони.

Задача 2. Визначте, чи подібні трикутники, якщо сторони:

а) 2см, 5см, 6см і 8см, 18см, 20см;

б) 5см, 8см, 9см і 15см, 24см, 27см.

Завдання 3. Знайти недосяжну відстань між домиками, якщо відстань від одного з них до лісу – 10 км, протяжність ділянки дороги, що проходити паралельно – 4км, а відстань від автобусної зупинки до лісу – 2 км.

Розв'язання:

Складемо математичну модель даного завдання. Накресліть малюнок.

1) Трикутники ACB і DCE подібні (за двома кутами), так як DE паралельно AB, а AB та DE січні.

2) Значить AB=20 (м)

Відповідь: 20м

Контрольна робота 3. "Подібність трикутників".

(О. М. Роганін. Комплексний зошит для контролю знань. Геометрія 8. Стор.45, 1 варіант. Задачі 1-3, 5-7)

👉ІІІ. Домашнє завдання.

Контрольна робота 3. "Подібність трикутників".

(О. М. Роганін. Комплексний зошит для контролю знань. Геометрія 8. Стор.45, 2 варіант. Задачі 1-3, 5-7)

Алгебра

Онлайн урок 16.05.22.

Тема: "Розв'язування задач за допомогою квадратних рівнянь"

👉І. Усно.

В якому випадку правильно виконано записи?

1) Умова задачі: «Одне число х, а друге па 3 більше, їхній добуток дорівнює 88» відповідає рівняння:

а) х(х – 3) = 88; б) х + (х + 3) = 88; в) х(х + 3) = 88; г) х – (х + 3) = 88.

2) Умова задачі: «Площа прямокутника дорівнює 32 см2, сума суміжних сторін — 12 см. Знайти сторони прямокутника» відповідає рівняння:

а) х + 32 = х + 12; б) х(12 + х) = 32; в) 32/х=12; г) х(12 – х) = 32.

👉ІІ. Вивчення нового матеріалу.

1. Підручник п.23, с.181-183. Задачі 1-3.

2. Письмово.

Складіть систему рівнянь з двома змінними та розвяжіть задачу.

Задача 1. Два мікроавтобуси вирушають з міста Київ до міста Львів. Швидкість першого на 10 км/год. більша, ніж швидкість другого. Тому перший мікроавтобус прибуває на місце на годину раніше, ніж другий. Визначте швидкість кожного мікроавтобуса, якщо відомо, що відстань від Києва до Львова 560 км.

Підказка. Нехай швидкість І автобуса х км/год, а ІІ автобуса - у км/год. Тоді відстань 560 км І автобус проїзжає за 560/х год, а ІІ - за 560/у год. Перший автобус прибуває на місце на годину раніше ніж другий. Складаємо рівняння. 560/у - 560/х = 1. Швидкість першого на 10 км/год більша, ніж швидкість другого, тоді складаємо рівняння. х - у = 10.

Задача 2. Для будівництва залізниці було виділено дві бригади будівельників. Отримане завдання вони повинні були виконати за 6 днів. Перша бригада може виконати все завдання на 5 днів раніше ніж друга. За скільки днів може виконати завдання окремо кожна бригада?

Підказка. Нехай вся робота (будівництво залізниці) дорівнює 1. Перша бригада виконає всю роботу за х днів, а друга - за у днів, працюючи окремо. Продуктивність праці (робота, виконана за одиницю часу) І бригади дорівнює 1/х , а ІІ бригади - 1/у. Отримане завдання вони повинні були виконати за 6 годин, то маємо рівняння: 1/х + 1/у = 1/6. Перша бригада може виконати всю роботу на 5 днів раніше, то маємо рівняння: у - х = 5.

Задача 3. Змішавши 20-відсотковий і 60-відсотковий розчини кислоти, отримали 800 г. розчину, що містить 30% кислоти. Скільки грамів кожного розчину змішали?

Підказка.

20% розчин 60% розчин Всього

x г. y г. 800 г (х + у = 800)

0,20x 0,60y 8000,30 (0,2х+0,6у=8000,3)

Задача 4. Катер проходить 66 км за течією річки і 54 км проти течії за 6 год., а 44 км за течією на 3 год. швидше, ніж 90 км проти течії. Знайдіть власну швидкість катера і швидкість течії.

Підказка. Нехай х – своя швидкість катера, у – швидкість течії. Тоді швидкість катера за течією річки (х+у) км/год, а проти течії – (х-у) км/год. Відстань 66 км за течією річки катер проходитиме за 66/(х+у) годин, а 54 км – за 54/(х-у) рік. Витрачає на це 6 рік. Складаємо рівняння. 66/(х+у) + 54/(х-у) 6. Аналогічно 90/(х-у) – 44/(х+у) = 3.

👉ІІІ. Домашнє завдання. Вивчити п.23, с.181-183, №779, №796, №793.

Геометрія

Урок 13.05.22.

Тема: "Повторення. Теорема Фалеса. Середня лінія трапеції та трикутника"
👉І. Усно.

1. §6; 7- повторити, с.38-47.

2. "Пригадайте головне"
- Сформулюйте теорему Фалеса.
- Що таке середня лінія трикутника?
- Яка залежність між периметром даного трикутника та трикутника, утвореного його середніми лініями?
- Сформулюйте властивості середньої лінії трикутника.
- Чи можна побудувати в трикутнику 4 середні лінії? Поясніть.
- Якщо всі середні лінії трикутника рівні, то яким буде цей трикутник?
- Дайте означення трапеції.
- Які види трапеції ви знаєте?
- Що таке середня лінія трапеції?
- Сформулюйте властивість середньої лінії трапеції.
- Хто (за думкою істориків) почав застосовувати основні геометричні інструменти – циркуль і лінійку?

👉ІІ. Письмово.

Накресліть малюнок до умови задачі. Розвяжіть задачу.

Задача 1. Середня лінія трикутника.
Дано: ∆АВС, АК = КВ, К∈АВ, М∈АС, Z∈CВ, КZ || AC, ZM || AB, P ΔКZМ= 20cм. Знайти: Р ∆ АВС

Відповідь: 40см.

Задача 2. Середня лінія трикутника

Дано: АВС,
МА = МВ = ВN = NC = MN =6cм,
Знайти: 1) сторони АВС , 2) кути АВС.

Відповідь: рівносторонній трикутник; 60˙

Задача 3. Середня лінія трапеції
Дано: АВСD -трапеція,
АM= МВ =СN= ND,
BК 丄АD, АК = 3, ВС = 7.
Знайти: МN.

Відповідь: 10см

Задача 3. Периметр трикутника дорівнює 68см, а довжини його середніх сторін відносяться як 4:6:7. Знайдіть сторони даного трикутника.
Дано: ∆АВС;
М-середина АВ;
К-середина ВС
Р-середина АС;
Р ΔАВС =54см;
КР:РН:КН=4:6:7
Знайти: АВ,ВС,АС.
Розв’язання.
Р=68:2=34(см)-вл.середньої лінії трикутника;
Введемо коефіцієнт пропорційності –х. Тоді:
4х+6х+7х=34
17х=34
х=34:17
х=2.
отже:
АВ=4∙2∙2=16см;
АС=6∙2∙2=24см;
ВС=7∙2∙2=28см.
Відповідь: 16см, 24см, 28см.
👉ІІІ.Домашнє завдання.
§6,7-повторити №298 (обов’язкове завдання для всіх,середній рівень),№260 (1), №309 (виконують учні, які бажають оцінку достатнього рівня), №323 (завдання високого рівня).

Урок 11.05.22.

Тема: "Квадратне рівняння як математична модель прикладної задачі"
👉І. Усно.

1. Розв'яжіть рівняння:

а) а2 - 4а + 3 = 0; б) у2 - 3у = 0; в) (у - 2) (у + 2) = 0;
г) (у - 3) (у + 2) = 6; д) х4 – х2 = 0.

2. За даною умовою складіть рівняння:

а) одне число х, інше х + 5 добуток 15;
б) довжина прямокутника а, ширина (а – 2), площа 48 см2;
в) гіпотенуза (прямокутного) трекутника х, катете (х – 1) і (х – 2).
Як записати теорему Піфагора для цього трекутника?

👉ІІ. Вивчення нового матеріалу.

1. Конспект
1. Загальний план
1) Позначити одну з величин літерою Х; виразити інші невідомі величини через Х. 2) Використавши дані в умові задачі величини (або співвідношення між ними), скласти рівняння. 3) Розв'язати складене рівняння. 4) Розтлумачити знайдені корені рівняння відповідно до умови завдання. Записати відповідь.
Схема розв'язання задач складанням рівняння

2. Вивчити п.23, с.181-183.

3. Письмово №777, №782.

👉ІІІ. Домашнє завдання. Вивчити п.23, с.181-183. Задачі 1-2. Повторити п.7. Письмове завдання №779, №784.

Геометрія

Онлайн урок 10.05.22.

Тема: "Повторення. Чотирикутники та їх властивості".

👉І. Усно.

1. Натисніть на посилання. Розвяжіть кросворд.

https://learningapps.org/display?v=pzwm9c1i322

2. У чотирикутнику точка перетину діагоналей ділити їх на чотири рівні відрізки. Якого вигляду цей чотирикутник?

3. Знайдіть у прямокутнику (рис. 1) всі рівні між собою кути. (Підказка. Протилежні сторони прямокутника паралельні. Кути 1 і 9 внутрішні різносторонні. Отже ∠1=∠9)

4. АВ - діаметр колу, в який вписано чотирикутник ADBC, причому AD = BC (рис. 2). Доведіть, що ADBC прямокутник. (Підказка. Кут АDВ, що спирається на діаметр АВ - прямий)

5. ABCD - ромб (рис. 3). Визначте угол х. (Підказка. Кути ромба, прилеглі до однієї сторони, у сумі складають 180 градусів)

6. ABCD - паралелограм, CM = CK (рис. 4). Доведіть, що ABCD – ромб. (Підказка. Доведіть, що протилежні сторони ВС і АD паралелограми рівні і паралельні)

👉 ІІ. Письмове.

1. За даними рис. 1 знайдіть куті паралелограма ABCD.

2. За даними рис. 2 знайдіть P паралелограма AВСD.

3. Точка перетину діагоналей прямокутника розташована від більшої сторони на 5 см ближче, ніж від меншої сторони. Знайдіть сторони прямокутника, якщо його периметр дорівнює 44 см.

4. На рис. 5 ABCD - прямокутник. Знайдіть куті х і у.

5 . На рис. 6 ABCD-ромб. Знайдіть куті х і у.

6. Висота, що проведена із вершини тупого угла ромба, ділити його сторону навпіл. Знайдіть:
а) куті ромба;
б) бік ромба, якщо його менша діагональ дорівнює 16 см.

👉ІІІ. Домашнє завдання. Повторити п.1-5, с.8-37. "Контрольні запитання" 1-7, с.66. Письмове "Тестові завдання" №1 (1-5), с.66.

Алгебра.

Урок 09.05.22.

Тема: "Розв'язування рівнянь, що зводяться до квадратних. Тест-контроль"

👉І. Усно.

1. Яку заміну слід виконати у рівнянні, щоб дістати квадратне рівняння:
а) ( х ² + 6 х + 9) – 2( х + 3) – 3 = 0;

б) ( х ² + 6 х ) ² - 2 ( х ²+ 6 х ) - 3 = 0.

2. Які квадратні рівняння дістанемо у завданні 1, якщо виконаємо відповідну заміну?

Перевір себе:

а) ( х + 3 ) ² – 2( х + 3) – 3 = 0;

ЯКЩО (x + 3) = t, ТО t ² - 2t – 3 = 0.

б) ( х ² + 6 х ) ² - 2 ( х ²+ 6 х ) - 3 = 0;

ЯКЩО ( х ² + 6 х )= t, ТО t ² - 2t - 3 = 0.

👉ІІ. Письмово.

1. У якому випадку правильно виконано записи? Запиши правильне розв'язання.
а) х ⁴ – 3 х ² + 2 = 0

Заміна: х²= t , х ⁴ = t²тоді t²– 3 t + 2 = 0 ; х₁= 1, х ₂ = 2.

Відповідь. 1; 2.

б) х⁴– 3 х ² + 2 = 0.

Заміна: х ² = t , х ⁴ = t²тоді t ² – 3 t + 2 = 0, t₁= 1, t₂= 2.

Обернена заміна: х ² = 1 або х ² = 2, маємо: х₁= 1, х ₂ = √2

Відповідь. 1; √2.

в) х ⁴ – 3 х ² + 2 = 0.

Заміна: х ² = t ( t ≥ 0), тоді t ² – 3 t + 2 = 0; t ₁ = 1, t ₂ = 2.

Обернена заміна: х ² = 1 або х ² = 2, маємо: х = ±1, х = 土 √2

Відповідь. ±1; ±√2.

2. Розв'яжіть рівняння. а) х4-5х2 +4 = 0; б) х4-7х2-18 = 0.

3. Розв'яжіть рівняння:

а) ; б)

а) Розв'язання.

☝ Пам'ятаємо - дріб дорівнює 0, якщо:
1) чисельник дорівнює 0,

2) знаменник не дорівнює 0.

1) х2-х = 0; х(х-1)=0; х=0 або х-1=0; х=1 .
2) х+4≠0; х≠-4

Відповідь: 0 та 1.

б) Розв'язання.

1) 3у2-5у-2 = 0; D=b2-4ac=25-43(-2)=25+24=49.
X1 = (5 +7) / 6 = 2; X2 = (5-7) / 2 = -0,5.

2) 4-у≠0; у≠4.

Відповідь: -0,5 та 2.

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSfj7LP8BFsBD8oV1GfN0BDPMPK1VlTlRMxsik00Qi4E6xcPAA/viewform?usp=sf_link

👉ІІІ. Домашнє завдання. Повторити п.21-22, с.166-174, №752 (1,7) (див. пр.4, с.173) №750 (6) (див. пр.1, с.172), №757 (1,2) (див.пр.3, ст.172).

Геометрія.

Урок 06.05.22

Тема: "Розв'язування задач на обчислення площ многокутників. Тест-контроль"

👉І. Усно.

1. Повторити п.20-24, с.146-178.

2. Повторення формул площ фігур.

На кожну парту видається набір формул (рис. 2) та набір карток із зображеннями геометричних фігур (рис. 3).

Протягом 3 хвилин для кожної геометричної фігури знайти відповідну формулу для обчислення її площі.

👉ІІ. Письмово.

1.

2. Скільки потрібно взяти плит квадратної форми з діагональю 0,5 м, щоб покрити ними двір площею 200 м2? (Відповідь: 1600 штук.)

3. Готельний хол має форму трапеції з основами 20 м і 10 м і висотою 8 м. Знайдіть площу ковроліна, необхідного, щоб застелити цей хол. (Відповідь: 120 м2)

4. Басейн має форму ромба. Довжина його діагоналей дорівнює 20 м і 16 м. Яку площу займе цей басейн? (Відповідь: 160 м2)

👉ІІІ. Натисніть на посилання. Пройдіть тест (Тестові завдання виконати письмово у зошиті)

https://docs.google.com/forms/d/e/1FAIpQLScCF_xh6AreBLgYuHdoyOp1J9V-8aEeYa_NvOUDnZ2JrI-8qA/viewform?usp=sf_link

👉 ІУ. Домашнє завдання. Повторити п. 20-24, с.146-178. Контрольні запитання 1-8, с.178. №1167 (1), №1107 (2), №1061.

Онлайн урок 04.05.22.

Тема: "Розв'язування рівнянь, що зводяться до квадратних"

👉І. Усно.

1. Скоротіть дроби:
; ; ; ; ; .
2. Знайдіть корені рівнянь:
х2 – 64 = 0; у2 + 49 = 0; 2р2 - 7р = 0; t2 = 0; 2х2 + 4х - 1 = 0; х2 + 3х + 4 = 0.
3. При яких значеннях змінної х вираз 3х – 1 набуває значень: 0; -2; 3; ?
4. Виконайте множення:
(x + 1)(x – 1); (x + 1) (x - 3); (x + 1) (x + 2); (x - 1) (x - 4).

👉ІІ. Вивчення нового матеріалу.

1. Підручник п.22, с.172-174.
2. Написати конспект.

ах4 + bх2 + с = 0 - біквадратне рівняння

Заміна: х2 = t (t ≥ 0)

ах4 + bх2 + с = 0 at2 + bt + c = 0

Шляхом рівносильних перетворень: дробово-раціональні рівняння:

рівняння вигляду , де P(х) і Q(х) — багаточлени від однієї змінної, рівносильні системі:

👉ІІІ. Письмове.

1. Розв'язування рівнянь різного виду, що зводяться до квадратних уведень нової змінної. Розв'яжіть рівняння:
а) (х2 – 1)2 – 11(х2 – 1) + 24 = 0, заміна х2 – 1=t;

б) (х2 + 2х)2 – 2(х2 + 2х) – 3 = 0, заміна х2 + 2х=t.

2. Розв'язування біквадратних рівнянь.
Розв'яжіть рівняння:

а) 2х4 - 9х2 + 4 = 0, заміна х2=t;

б) 36х4 - 7х2 - 4 = 0.

👉ІУ. Домашнє завдання. Вивчіть п. 22, №751 (непарні), №753 (1,3).

Онлайн урок 03.05.22

Тема: "Розв'язування задач на обчислення площ многокутників"

👉І. Усно.

1. Повторити п.20-24, с.146-178.

2. Повторення вивченого с. 183 (формулі площ фігур)

👉ІІ. Письмово.

1. Визначте кількість сторін опуклого многокутника, сума кутів якого дорівнює 1080°.

Розв'язання.

Сума кутів опуклого многокутника обчислюється за формулою 180 (n - 2), що за умовою дорівнює 1080, де n - кількість сторін многокутника. Отже 180 (n – 2) = 1080

n - 2 = 1080: 180
n - 2 = 6
n = 8

Відповідь. 8 сторін

2. Площа квадрата дорівнює 144 см2. Знайдіть площу прямокутника, ширина якого менша від сторони квадрата на 2 см, а довжина більша за сторону квадрата вдвічі.

Розв'язання.

Площа S кв. = 144 см2 = а2, тоді сторона квадрата а = 12 см.

S пр. = ab, длина а = 12 - 2 = 10 см, ширина b = 12 * 2 = 24 см.

S пр 10*24 = 240 см2

Відповідь. Площа прямокутника 240 см2.

3. У рівнобедреному трикутнику бічна сторона відноситься до основи як 5 : 6. Знайдіть площу трикутника, якщо висота, проведена до основи, дорівнює 8 см.

Розв'язання.

Нехай х - коефіцієнт пропорційності, тоді довжина бічної сторони ВС = ВА = 5х см, а основи АС = 6х см. У рівнобедреного трикутника висота ВD , проведена до основи, є медіаною. Отже половина основи АD = DC = 3х см.

За теоремою Піфагора з ΔВDC (∠D = 90) BD2 + DC2 = BC2. Висота трикутника ВD = h = 8 см. Маємо рівняння:
64 + (3х) 2 = (5х) 2;
64 + 9х2 = 25х2;
64 = 25х2 – 9х2;
64 = 16х2;
х2 = 64: 16;
х2 = 4;
х = 2.
2) DC = AD = 2 см, AC = AD + DC = 2 + 2 = 4 см.
Площа S тр. = 0,5 аh = 0,5 * 4 * 8 = 16 cм2.
Відповідь. 16 см площа трикутника.

4. Знайдіть кут ромба, якщо його висота дорівнює 5 см, а площа — 50 см2.

Розв'язання.
Висота ромба ВМ = h = 5 см, площа ромба S = аh = 50 см2. Тоді маємо рівняння:
50 = 5а;
а = 50: 5;
а = 10 см – сторона ромба.
У трикутника ВМА (∠М = 90), проти кута А лежить катет ВМ = 5 см, у два рази менший за гіпотенузу ВА = а =10 см. Тоді ∠ А = ∠С = 30 градусів (протилежні кути ромба рівні). У ромба кути, прилеглі до бічної сторони, внутрішні односторонні. Їхня сума 180 градусів. Тоді ∠ АВС = ∠ АДС = 180 – 30 = 150 градусів.
5. У паралелограма АВСD з вершини тупого угла В проведено висоти ВK та ВМ (див. рисунок). ВK=16 см, AK=12 см, ВМ=24 см.
1. Визначте довжину сторони АВ (у см). 2. Обчисліть площу паралелограми АВСD.

Розв'язання.
АВ гіпотенуза ∆ВКМ, ∆ВКМ-прямокутний.
За теоремою Піфагора
АВ²=ВК²+АК²=16²+12²=256+144=400
АВ=√400=20 cм
AB=CD=20cм
S=CDBM=2024=480 cм² площа паралелограма.

👉ІІІ. Домашнє завдання. Повторити п. 20-24, с.146-178. Контрольні запитання 1-8, с.178. Тестові завдання 1-5, с.178.

Онлайн урок 02.05.22

Тема: "Розкладання квадратного тричлена на множники. Тест-контроль"

👉І. Усно.

1. Корені квадратного тричлена дорівнюють – 8 і 0,5, а старший коефіцієнт – 3. Запишіть цей тричлен у вигляді добутку

1. Корені квадратного тричлена дорівнюють – 0,3 і 7, а старший коефіцієнт – 5. Запишіть цей тричлен у вигляді добутку

2. Розкладіть на множники тричлени:

2х2 - 3х + 1

3х2 - 2х - 1

👉ІІ. Письмово.

1. Розкладіть на множники многочлен:

а) 2х2 – 18; б) 4х2+4х+1; в) 4х3 – х2; г) х2 – 5х + 6.
2. Скоротіть дроб: а) ; б) .
3. Знайдіть корені квадратного тричлена: а) х2 – 5х + 6; б) х2 – 5х; в) х2 – 6; г) 3х2 – 4х + 1.
4. Заповніть перепустки: а) х2 + 3х + 2 = (х – …)(х + 1); б) 2х2 - 3х + 1 = 2 (х - 1) (х - ...).
5. Скоротіть дроб: а) ; б)

👉ІІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLScmW3hLuJCgkvIiIirbn5bcv4X5g46wkgWWVyg2ZbhCsZy49w/viewform?usp=sf_link

👉ІУ. Домашнє завдання. Повторити п.21, с.166-168, Тестові завдання виконати письмово у зошиті.

Геометрія.

Урок 29.04.22

Тема: "Площа трикутника, ромба, трапеції. Розв'язування задач. Тест-контроль"

👉І. Усно.

Встановіть відповідність між твердженнями 1) – 7) і твердженнями а) – з).

1) Площа трикутника дорівнює...
2) Площа трапеції дорівнює...
3) Площа паралелограма дорівнює...
4) Площа ромба дорівнює...
5) Площа квадрата дорівнює...
6) Площа прямокутника дорівнює...
7) Площа прямокутного трекутника дорівнює...

а) здобутку двох сусідніх його сторін;
б) половині видобутку діагоналей;
в) половині видобутку висоти на бік, до якої проведена висота;
г) видобутку сторони на висоту;
д) добування висоти на бік, до якої проведена висота;
є) видобутку середньої лінії на висоту;
ж) квадрату його сторони;
з) половині видобутку катетів.
2. ☝Повторити формули площ фігур (підручник, форзац №2). Знайдіть площу фігур, зображених на рисунку 1. Перевір себе.
S = (3+5)/22 = ...
S = 1/2 2 * 5 = ...
S = 1/2 * 3 * 4 = ...
S = 3 * 2 =...
S = 4 * 6 =...
Рис. 1

👉ІІ. Виконання письмових вправ.

1. Знайдіть площу прямокутного трикутника з гіпотенузою 26 см і катетом 10 см (Вказівка. Знайдіть інший катет прямокутного трикутника за теоремою Піфагора та застосуйте формулу для площі прямокутного трикутника).

2. Знайдіть сторону ромба із площею 96 см2 і діагоналлю 16 см (Вказівка. Знайдіть другу діагональ ромба, застосувавши формулу для площі роба S =1/2 d1*d2, де d1, d2 діагоналі ромба).

3. Менша основа і бічна сторона прямокутної трапеції дорівнюють а см, а один із кутів — 45°. Знайдіть площу трапеції.

👉ІІІ. Натисніть на посилання. Виконайте тест.

https://docs.google.com/forms/d/e/1FAIpQLSdXj2Ry99nncxbf85p3FkPf3mLFkr7JBm6bzdxjaI-5ohCaIw/viewform?usp=sf_link

👉ІУ. Домашнє завдання. Повторити п. 20-24, с.146-178. Контрольні запитання 1-8, с.178. Розв'язати тестові завдання.

Алгебра.

Урок 27.04.22

Тема: "Розкладання квадратного тричлена на множники"

👉І. Усно.

Якщо х1 і х2 – корені квадратного тричлена а х2 + bх + с, то а х2 + bх + с = а (х – x1) (x – x2) .

Приклад 1. Розкласти на множники квадратний тричлен:

Розв'язання.

1) Коренями рівняння є числа х1 = -2,5; х2 = 1. Тому знайдений результат можна записати інакше, помноживши на -2 двочлени (х + 2,5); (х-1). Маємо

2) квадратне рівняння 2 х2 - 12х + 18 = 0 має два рівні корені х1 = х2 = 3. Тому

Приклад 2. Зменшити дроб.

Квадратне рівняння 2 х2 - 2х - 4 = 0 є числа 2 і -1.

Отже,

👉ІІ. Виконання вправ.

1. Корені квадратного тричлена дорівнюють – 8 і 0,5, а старший коефіцієнт – 3. Запишіть цей тричлен у видобутку

2. Корені квадратного тричлена дорівнюють – 0,3 і 7, а старший коефіцієнт – 5. Запишіть цей тричлен як видобутку

3. Розкладіть на множники тричлен: 2 х2 - 3х + 1; 3 х2 - 2х - 1.

4. Самостійна робота.

Варіант 1	Варіант 2
1. Розкладіть на множники:
а) х2 - 16х + 63; б) 3x2 + x – 2	а) х2 - 12х + 35; б) 3х2 + 7х - 6
2. Скоротіть дроб

👉ІІІ. Домашнє завдання. Вівчіті п.21, с.166-168. №729 (пеарні), №733, №737 (1).

Геометрія.

Урок 26.04.22.

Тема: "Площа трапеції"

👉І. Перевірка домашнього завдання.

Тестове завдання.

Варіант І

1. Назвіть формулу площі прямокутника зі сторонами а і b.
а) ab/2; б) (a + b)/2; в) а2+b2; г) ab.

2. Знайдіть площу ромба ABCD, якщо АС = 5 см, BD = 8 см.
а) 20 см2; б) 40 см2; в) 10 см2; г) 13 см2.

3. За даними зображення знайдіть площу трекутника ABC.
а) 42; б) 84; в) 13; г) 21.
4. Знайдіть площу прямокутника зі стороною 5 м і діагоналлю 13 м. а) 60 см2; б) 60 м2; в) 65 м2; г) 156 м2.

5. Дві сторони трекутника дорівнюють 8 см і 12 см, а висота, проведена до меншої з них, — 3 см. Знайдіть висоту, проведену до більшої сторони.
а) 4 див; б) 2 див; в) 45 см; г) 10 див.

6. Знайдіть площу ромба зі стороною 12 см і гострим кутом 30°.
а) 144 см2; б) 36 см2; в) 72√3 см2; г) 72 см2.

Варіант 2

1. Назвіть формулу площі квадрата зі стороною а.
а) 2а2; б) 4а; в) а2; г) 4а2.

2. У паралелограмі ABCD до сторони AD проведено висоту ВК. Знайдіть площу паралелограма, якщо ПС = 8 см, ВК = 5 см.
а) 20 см2; б) 40 см2; в) 80 см2; г) 13 см2.

3. За даними малюнка знайдіть площу три кутника ABC.
а) 30; б) 60; в) 15; г) 11.
4. Знайдіть площу прямокутного трекутника з катетом 15 м і гіпотенузою 17 м. а) 127,5 м2; б) 60 м2; в) 120 м2; г) 60 см2.

5. Сторони паралелограма дорівнюють 12 см і 16 см, а менша висота – 3 см. Знайдіть більшу висоту паралелограма.

а) 4 див; б) 2,25 див; в) 6 см; г) 14 див.

6. Знайдіть площу паралелограма зі сторонами 8 м і 12 м та гострим углом 30°.

а) 48 м2; б) 96 м2; в) 24 м2; г) інша відповідь.

👉ІІ. Вивчення нового матеріалу.

1. Підручник п.24, с.172.

☝Теорема (про площу трапеції). Завдання.

2. ☝Формула: S = (a + b)/2*h, a, b – основи трапеції, h – висота трапеції. Або: площа трапеції дорівнює видобутку середньої лінії на висоту.

3. Виконання усних вправ.

1) Дві рівновеликі трапеції мають рівні висоти. Чи означає це, що основи даних трапецій також відповідно рівні?

2) Чи може діагональ трапеції ділити її на два рівновеликі трекутники? Відповідь обґрунтуйте.

3) Дано: ABCD - трапеція (BC | | AD). Знайдіть S, якщо:
а) ПС = 2 см; AD = 10 див; h = 5 див;
б) BC + AD = 16 див; h = 6 див;
в) середня лінія дорівнює 10 см; висота 5 см;
г) r = 5 см; AB+CD=18.

4. Виконання листових вправ.

1) Знайдіть площу трапеції, якщо:
а) її основи дорівнюють 4 см і 10 см, а висота — 6 см;
б) висота трапеції та її середня лінія дорівнюють 8 см.

2) Основи рівнобедреної трапеції дорівнюють 8 см і 16 см, а гострий угол — 45°. Знайдіть площу трапеції.

3) Знайдіть площу:
а) рівнобедреної трапеції з основами 15 см і 39 см, діагональ якої перпендикулярна до бічної сторони;
б) прямокутної трапеції з бічними сторонами 12 см і 13 см, діагональ якої є бісектрисою острого угла.

👉ІІІ. Домашнє завдання. Вівчіті п.24, с.172. №1148, №1150, №1152.

Онлайн урок 25.04.22

Тема: "Розкладання квадратного тричлена на множники"

👉І. Усно.

1. Не розв'язуючи рівняння, знайти суму і добуток його коренів:

1) х 2 – 12х + 18 = 0;

Розв'язання. За теоремою Вієта: х 1 + х 2 = 12; х 1 * х 2 = 18.

2) 3х2 + 7х + 2 = 0;

Розв'язання.

Поділимо кожний додаток на число 3. Дістанемо рівняння: х2 + 3,5х + 2/3 + 0; х1 + х2 = -3,5; х1 * х2 = 2/3.
2. Користуючись теоремою, оберненою до теореми Вієта, встановити, чи є корінням рівняння : 1) х 2 + 2х + 3 = 0 числа 1 і 2. Розв'язання.

х 1 + х 2 = 1 + 2 = 3 ≠ -2. Отже числа 1 і 2 не є корінням рівняння.
2) х 2 – 5х + 6 = 0 числа 2 та 3.
Розв'язання.

х 1 + х 2 = 2 + 3 = 5; х1 * х2 = 2 * 3 = 6. Отже числа 2 і 3 є корінням рівняння.
3. Число 7 є коренем рівняння х 2 + рх - 42 = 0. Знайти значення р і другий корінь рівняння.
Розв'язання.
х 1 = 7; х1 * х2 = -42; 7*х2 = -42; х2 = -6;
х 1 + х2 = 7 – 6 = 1.
Відповідь. х2 = 6; р = -1.

👉ІІ. Вивчення нового матеріалу.

1. Способи розкладання квадратного тричлена на множники.

Приклад 1. Розкласти на множники квадратний тричлен способом групування: х2 – 5х – 36 = х2 – 9х + 4х – 36 = х(х – 9) + 4 (х – 9) = (х – 9)(х + 4).

Теорема (для розкладання квадратного тричлена на множники).

☝ Якщо х1 і х2 – корені квадратного тричлена, то ах2 + bx + cx = a (x – x1)(x – x2).

Якщо відомі корені квадратного тричлена, то його можна розкласти на лінійні множники.

Зауваження. Якщо дискримінант квадратного тричлена дорівнює нулю, то

вважають, що квадратний тричлен має два рівні корені, тобто х1 = х2. У цьому випадку розклад квадратного тричлена на множники має такий вигляд:

ах 2 + bх + с = а (х – х1) 2 .

Приклад 2. Розкласти квадратний тричлен х2 – 12х + 35 на множники.

Розв'язання. Розв'яжемо відповідне квадратне рівняння: х2 - 12х + 35 + 0. З теореми, оберненої до теореми Вієта маємо:

х1 + х2 = 12; х1 * х2 = 35. Отже х1 = 5, х2 = 7.

Отримаємо розклад:

х2 - 12х + 35 = (х - 5) (х - 7).

2. Підручник. Вивчіті п. 21 (приклади 1, 2, 3), с.166-168. Відповісти на запитання 1-7, с.168.

3. Письмове №728 (1,3,5,7) (дивись приклад 1), №730 (1,3,5) (дивись приклад 2), №734 (1) (дивись приклад 3).

4. Математичний диктант.

Варіант 1

1. Квадратний тричлен -х2 – ах – з має корені - 63 і 2. Розкладіть цей тричлен на множники

2. Квадратний тричлен подали у вигляді видобутку

3(х – 5)(х + 9). Назвіть корені цього тричлена та його перший (старший) коефіцієнт

Варіант 2

1. Квадратний тричлен -2х2 + ах + з має корені 12 і - 31. Розкладіть цей тричлен на множники

2. Деякий квадратний тричлен подали у вигляді видобутку

4(х + 8)(х – 19). Назвіть корені цього тричлена та його перший (старший) коефіцієнт

👉ІІІ. Домашнє завдання.

Вівчіті п.21, с.166-168., №729 (непарні), №731, №735 (1).

Геометрія.

Урок 22.04.22.

Тема: "Площа ромба"

👉І. Усно.

1. У паралелограмі зі стороною а проведеною до неї висотою ha і площею S знайдіть:

а) S якщо а = 10 см, ha = 6 см;

б) а якщо S = 48 см2, ha = 4 см;

в) ha якщо S = 120 см2, а = 24 см.

2. Діагональ паралелограма дорівнює 15 см і перпендикулярна його стороні. Знайдіть площу паралелограма, якщо інша його сторона дорівнює 17 см.

👉ІІ. Вивчення нової теми.

1. Підручник п. 22, с.160 (теорема про площу ромба. Наслідок).

2. Натисніть на посилання. Продивіться відео. Законспектуйте розв'язок задач з відео.

https://youtu.be/pJGfdcxIpl0

3. Письмове №1060, №1064, №1071.

👉ІІІ. Домашнє завдання. Вівчіті п22, с.160 (теорема про площу ромба) №1061, №1063, №1076(1).

Алгебра.

Онлайн урок 20.04.22.

Тема: "Квадратний тричлен та його корені"

👉І.Перевірка домашнього завдання.

Виконати самостійну роботу на тему "ТЕОРЕМА ВІЄТА".

1) Знайдіть суму та добуток коренів квадратного рівняння 3х2 – х – 24 = 0. (3б)

А) - 1/3; - 8, Б) – 1/3; 8, В) 1/3; - 8; г) 1/3;8.

2) Знайдіть коефіцієнти b і c рівняння х2 + bx + c = 0, якщо його корінням є числа - 6 і 3. (3б)

а) b = 3; с = - 18; Б) b = 3; с = 18; В) b = - 3; с = - 18; Г) b = = - 3; з = 18.

3) Один із коренів квадратного рівняння х2 – 7х + q = 0 дорівнює 9. Знайдіть коефіцієнт q та другий корінь рівняння. (5б)

👉ІІ. Вивчення нового матеріалу.

1. Натисніть на посилання. Продивіться відео.

https://youtu.be/UVkeH46hyWg

2. Підручник:

1) Вівчіті п.21, с.166 (до теореми 21.1).

2) написати конспект.

Квадратним тричленом називається багаточлен вигляду ax 2 + bx + c, де x — змінна, a , b і c — деякі числа-коефіцієнти, при цьому a ≠ 0. Корінням квадратного тричлена називаються числа, за яких тричлен дорівнює нулю.

Отже, щоб знайти корені квадратного тричлена, треба скласти відповідне йому квадратне рівняння (у лівій частині даний тричлен, у правій — нуль) і розв'язати його. Корені квадратного рівняння будуть корінням відповідного квадратного тричлена.

Якщо х таке, що ах2 + bх + с = 0, то х — корінь квадратного тричлена ах2 + bх + с.

3. Письмове.

1) Чи має квадратний тричлен корені? Якщо має, то скільки:

a) x2 - 2x + 1; б) x2 – 5; в) х2+1; г) 3x – x2.

2) Чи є число 1; 0; -1/2 коренем квадратного тричлена:

а) 2х2 - 5х + 3; б) ; в) х2 – х?

3) Знайдіть корені квадратного тричлена:

а) x2 + х – 12; б) х2 – 2х – 35; в) 3х2 + 16х + 5; г) х2 + 3х + 2;

д) х2 - 10х + 18; є) 2х2 – 3х + 1.

4. Натисніть на посилання. Перевірте собі.

https://learningapps.org/display?v=p8xu6d7

👉ІІІ. Домашнє завдання. Вівчіті п.21 (до теореми 21.1), №726, с.168.

Геометрія.

Урок 19.04.22.

Тема: "Площа трекутника. Розв'язання задач"

👉І. Усно.

1. Підручник. Повторити п.23, с.165-166.

2. Стр. 200, задачі 1-3.

3. Натисніть на посилання. Продивіться відео.

https://youtu.be/COh6T4cK67E

👉ІІ. Письмове.

1. Записати розв'язок задач з відео.

2. Один з катетів прямокутного трекутника дорівнює 24 см , а гіпотенуза – 25 см . Знайдіть площу прямокутного трекутника.

3. Сторона трекутника втричі більша за висоту, яка проведена до цієї сторони. Знайдіть висоту, якщо площа трекутника дорівнює 24 см2 .

4. Знайдіть площу прямокутного трекутника, катете якого дорівнює 8 см і 12 см .

5. Площа трикутника дорівнює 50 см2 . Знайдіть висоту трекутника, якщо сторона, до якої вона проведена, дорівнює 5 см .

6. Знайдіть площу трекутника, якщо висота дорівнює 10 см , а сторона до якої проведена висота – 6 см .

👉ІІІ. Домашнє завдання.

Повторити п.20-23, с.146-171, №1099, №1101, №1107, №1124.

Урок 18.04.22

Тема:"Формула коренів квадратного рівняння. Тест-контроль"

👉І. Усно.

1. Повторити п.18-20, с.141-164.

2. Натисніть на посилання. Продивіться відео.

https://youtu.be/mwVdPl6wtPg

👉ІІ. Письмово записуйте приклади з відео у робочу тетрадь.

👉ІІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSfocwpkumpRPLloXqIxs7GDIhgys_wMVyTnW6pTfD-XaIGydw/viewform?usp=sf_link

👉ІУ. Домашнє завдання. Повторити п.18-20, с.141-164. Письмово виконати тестові вправи.

Геометрія

Урок 15.04.22.

Тема: "Площа трекутника"

👉І. Усно.

Завдання. На рис. зображено дві фігури: паралелограм ABCD і трекутник MNK такі, що AD = МК, і висоти проведені до цих сторін (ВН, NF), також рівні (див. рис). Проведіть діагональ BD паралелограма та порівняйте площі трекутника та паралелограма. 👉ІІ. Вивчення нового матеріалу.

Підручник п.23, с.168-166.

1. Теорема (формула площі трикутника), с.165.
2. Площа прямокутного трекутника: S = 1/2 ab, де а, b катете прямокутного трекутника.
3. Площа рівностороннього трекутника: №1105, с.168.
4. Властивість медіані трикутника.
5. Завдання с.166.
☝Щоб усвідомити логічні зв'язки між вивченими на уроці формулами, записи цих формул можна записати у вигляді схеми, рис. 👉ІІІ. Письмове.

1. За даними малюнку 8 знайдіть площу трекутника ABC. 2. Знайдіть площу: а) рівнобедреного трекутника з основою 10 см і боковою стороною 13 см; б) прямокутного трекутника, гіпотенуза якого ділиться висотою на відрізки завдовжки 9 см і 4 см (повторити середні пропорційні у прямокутному трекутнику, с.100) ; в) рівностороннього трекутника з висотою 2√3 см.

👉ІІІ. Домашнє завдання. Вівчіті п.23, с.165-166, №1095, №1097, №1106, №1123 (1).

Алгебра.

Онлайн урок 13.04.22

Тема: "Формулі коренів квадратного рівняння. Розв'язання рівнянь".

👉І. Усно.

1. Перевірка домашнього завдання.

2. Натисніть на посилання. Подивіться відео.

1) https://youtu.be/N9NU3dy_RAs

2) https://youtu.be/bUA4_ynbFpU

3. Чому дорівнює змінна?

2х = 64; х2 = 16; 2х2 = 20; 21х2-х = 0.

4. Повторити теоретичний матеріал.

☝1. Квадратним рівнянням називається рівняння виду

ах2+ bх + с = 0 (1), де х – змінна, а, b і с – деякі числа, причому а ≠ 0.

Числа а, b і с – коефіцієнти квадратного рівняння (а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член).

Наприклад, - х2 + 6х + 1,4 = 0; 8х2-7х = 0.

Якщо а = 1, то квадратне рівняння (1) називається зведеним.

Якщо у квадратному рівнянні aх2 + bx + c = 0, хоча б один із коефіцієнтів bic = 0, то такі рівняння називаються неповними квадратними рівняннями.

👉ІІ. Письмове.

1. Чи є квадратним рівняння? Якщо так, то вкажіть його коефіцієнти:

а) 3,7 х2 - 5х + 1 = 0; б) 48х2 - х3-9 = 0; в) 1 - 12х = 0;

г) 7х2 - 13 = 0; д) - х2 = 0?

2. Вкажіть, які з даних рівнянь є зведеними, і перетворіть незведені рівняння у зведені:

а) 5х2 - 9х + 4 = 0; б) х2 + 3х - 10 = 0;

в) - х2 - 8х + 1 = 0; г) 6х2 - 30х = 0; ґ) 9х2 = 0.

3. Правильно ли записано дискримінант, обчисліть, якщо можливо :

1) 2х ² + 3х - 1 = 0, Д = 3 ² - 4 · 2 (-1);

2) 3х ² - 4х + 2 = 0, Д = (-4) ² - 24;

3) -1/2х ² - 5х +3 = 0, Д = (-5) ² - 12 (-1/2);

4) 1/4 х ² + 2х - 4 = 0, Д = 2 ² + 4 · 1/4 (-4).

5. Розв'яжіть рівняння.

1) х ²+ 20х + 91 = 0; 2) х ²- 20х + 91 = 0;

3) х ²+ 16х +55 = 0; 4) х ²- 18х +80 = 0.

👉ІІІ. Домашнє завдання.

Повторити п.18-20, с.141-164. Письмове с.165, завдання №5 "Перевір собі" у тестовій формі.

Геометрія.

Урок 12.04.22.

Тема: "Площа паралелограма. Розв'язання задач".

👉І. Усно.

1. Повторити п.20-22, с.146-164.

2. Відповісти на запитання 1-6 с.148, 1-6 с.155, 1-5 с.161.

3. ☝Формулі.

1) Площа паралелограма дорівнює S=ah , де a – довжина сторони паралелограма, h – довжина висоти, проведеної до цієї сторони.

2) Площа квадрата дорівнює S = a2 , де а - Сторона квадрата;

S = 1/2, d1, d2, де d1, d2 - діагоналі квадрата.

3) Повторити формули: підручник п.14, с.99.

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLScbcqaHJ8bUIVKSS33cBvMWkDkpYrc1y1BWpu9CRaVhcyjvHg/viewform?usp=sf_link

👉ІІІ. Домашнє завдання.

Повторити п. 20-22, с.146-164. Письмове:

1. Обчисліть площу паралелограма, якщо одна з його сторін 8 дм, а висота проведена до цієї сторони, що дорівнює 6 дм.

а) 24дм2 б) 48 дм2 в) 64 дм2 г) немає правильної відповіді

2. Знайдіть площу квадрата, якщо його периметр 36см.

а) 81см2 б) 18 см2 в) 36 см2 г) немає правильної відповіді

3. Менша сторона прямокутника дорівнює 6 см, а друга сторона на 2 см більша. Чому дорівнює площа прямокутника?

а) 60см2 б) 48 см2 в) 24см2 г) немає правильної відповіді.

Алгебра.

Урок 11.04.22

Тема: "Теорема Вієта та теорема, обернена до теореми Вієта".

👉І. Усно.

1. Розв'яжіть рівняння:

а) х2 – 25 = 0; б) а2 - 5а = 0; в) у2 + 9 = 0; г) n2 - 19 = 0; д) 5х2 = 0,2.

2. Назвіть перший, другий коефіцієнти і вільний член квадратного рівняння:

а) а2 + 4а - 1 = 0; б) у2 - 3 = 0; в) 2b2 - 5b = 0; г) 3 - 2х2 - х = 0; д) 3с2 = 0.
3. Знайдіть значення виразів: ; ; ; ; ; .

👉ІІ. Засвоєння знань.

1. Підручник п.20, с.157-160.

1) Теорема 20.1 (теорема Вієта).

☝Якщо ах2 + bх + с =0 має корені х, і х2 (D >0), то


	;

2) Наслідок.

☝Якщо х2 + рх + q = 0 має корені х1 і х2 (D > 0),

то х1 + х2 = -Р; х1 · х2 = q

3) Теорема 20.2 (обернена до теореми Вієта).

4) Наслідок.

Обернена теорема:
		☝Якщо числа m і n такі, що m + n = -p, mn = q, то

		m і n - корені рівняння х2 + pх + q = 0

5) Приклади 1-4.

6) Розв'язування зведених квадратних рівнянь «підбором».
х2 - 2х - 3 = 0: х1 + х2 = 2, х1 · х2 = -3 х1 = 3, х2 = -1.

👉ІІ. Письмове.

1. Складіть зведене квадратне рівняння, в якому сума р і добуток q його коренів дорівнюють:
а) р = - 5; q = 4; б) р = 15; q = -6; в) р = - 5; q = 0; г) p = 0; q = -2.

Розв'язання.

а) Зведене квадратне рівняння має виглад х2 + рх + q = 0;

р = -5; q = 4 і х2 – 5х + 4 = 0.

2. Один із коренів квадратного рівняння х2 + 4х – 21 = 0 дорівнює - 7. Знайдіть другий корінь.

Розв'язання.

Якщо х2 + рх + q = 0 має корені х1 і х2 (D> 0), то х1 + х2 = -р = -4;

х1 · х2 = q = -21. Один з коренів дорівнює -7, тоді

-7 + х2 = -4, -7 х2 = -21 і х2 = -4 + 7 = 3.

3. Є дані числа коренями квадратного рівняння із заданими коефіцієнтами?
а) х2 - 2,5 х + 1 = 0, числа 2 і 0,5; б) х2 + 20х - 125 = 0, числа -5 і 25.

Розв'язання.

а) Якщо х2 + рх + q = 0 має корені х1 і х2 (D > 0),

то х1 + х2 = -p = 25; х1 · х2 = q = 1,

тоді 2+0,5 = 2,5 і 2*0,5 =1. Дані числа є корінням рівняння.

4. Знайдіть за формулою корені рівняння і виконайте перевірку за теоремою, оберненою до теореми Вієту:
а) х2 – 13х + 40 = 0;
б) х2 + 6х + 5 = 0.

5. Розв'яжіть рівняння і виконайте перевірку за теоремою, оберненою до теореми Вієта:
а) х2 – 2х – 9 = 0;
б) 3х2 - 4х - 4 = 0.

👉ІІІ. Домашнє завдання. Вівчіті п.20, с.157-160. Приклади 1-4. №683, №685, №689.

Геометрія

Урок №2: 08.04.22.

Тема: "Площа паралелограма".

👉І. Усно.

Повторення формул. Перевірка домашнього завдання.

Ви як думаєте, що треба перш за все знати, щоб виміряти площу земельної ділянки? (форму)

1) Ділянка має форму квадрата зі стороною 50м. Проблема розв'язується, якщо ділянка має форму квадрата S=a2.

2) Ділянка має форму прямокутника зі сторонами 30м та 50м. Проблема розв'язується, якщо ділянка має прямокутну форму S=ab.

3) Ділянка має форму прямокутного трекутника з катетами 60м та 40м. Проблема розв'язується, якщо ділянка має форму прямокутного трекутника S=1/2 ab , a,b катети прямокутного трекутника.

4) Ділянка має форму паралелограма. Довжина сторін – 40м і 20м, а відстань між довшими сторонами – 15м. Чи можемо ми розв'язати проблему?

👉ІІ. Вивчення нової теми.

1. Вивчіті п.22 (с.159-161), теорема ( для площу паралелограма) .

2. Завдання (с.160).

3. "Пригадайте головне" 1-2, (с.161).

4. Усно №1042.

5. Письмове.

1) Відпрацювання оформлення запису завдання у зошиті.

Задача: Сторона паралелограма дорівнює 8,1см, а його діагональ, що дорівнює 14 см, утворює з нею кут 30°. Знайти площу паралелограма.

Дано: ABCD – паралелограм, AC=14 см, DC=8,1см, ∠ACD=30˚

Найти: S(ABCD).

Розв'язання.

1. Проведемо AP丄DC.

2. З ΔAPC(∠P=90˚): АР=1/2 АС=1/2*14=7 см, як катет, що лежить проти кута 30˚.

3. S(ABCD)=DCAP=8,17=56,7(см 2).

Відповідь: 56,7 см 2 .

2) Розв'язання задач: №1045, №1047, №1051 (1, 2), 1056 (1).

👉ІІІ. Домашнє завдання.

П.22 (с.159-161), №1046, №1048, №1052, №1057.

Алгебра.

Урок 05.04.22.

Тема: "Розв'язування квадратних рівнянь".

👉І. Усно.

1. Математичний диктант

1) Квадратним рівнянням називається рівняння виду . . .

2) Число з називається ...
3) Записати формулу знаходження дискримінанту .
4) Якщо дискримінант дорівнює нулю, то рівняння має ...
5) Записати формули обчислення коренів квадратного рівняння.
6) Розв'язати рівняння :ах ² + вх = 0
7) Квадратне рівняння називається неповним, якщо . . .
8) Число називається . ..
9) Квадратне рівняння має два корені, якщо . ..
10) Розв'язати рівняння :ах ² +с =0
2. Оберіть правильну відповідь.
АТ 1 АТ 2 АТ 3 АТ 4
1) (х-4) (х +11) = 0 1) (х-1) (х-9) = 0 1) (х+3)(х-4)=0 1) (х +5) (х-7) = 0
а) 4; 11 а) 1; -9 а) -3; -4 а) -5; -7
б) -4;-11 б) -1; 9 б) 3; -4 6) 5; 7
в) 4;-11 в 1 ; -9 в) -3; 4 в) 5; -7
г) -4; 11 г) 1; 9 г) 3; 4 г) -5; 7
2) х(х+0,5)=0 2) (х-0.1) х = 0 2) х(х-0.3)=0 2) (х +0.7) х = 0
а) 0; -0.5 а) 0.1 а) 0; 0.3 а) 0
6) 0 6) 0.1; 0 6) 0.3 6) -0.7; 0
в) -0.5 в) 0 в) 0; -0.3 в) 0; 0.7
г) 0; 0.5 г) -0.1; г) 0 г) -0.7
3) х ² -2х = 0 ' 3) х ² +Зх = 0 3) х ² - 5х = 0 3) х ² +7х = 0
а) 0; -2 а) 0; 3 а) -5 а) 0
6) 0 6) 0 6) 0; -5 6) 0; 7
в) 0; 2 у 3 в) 0; 5 о 7
г) 2 г) 0; -3 г) 0 г) 0; -7
4) 9х2-1 ⁼ 0 4) 16х2 ^-9 = 0 4) 25х2-4 ⁼ 0 4) 4х2-1 ⁼ 0
а) -1/3; 1/3 а) 9/16 а) 6 1/4 а) -2; 2
6) 1/9 б) -3/4; 3/4 6) -4/25; 4/25 6) нема розв'язку
в) нема розв'язку в) -11/2; 11/2 в) -2/5; 2/5 в) 4/9
г) -3; 3 г) нема розв'язку г) нема розв'язку г) -1/2; 1/2
5) 2,7 х ² =0 5) -0.07х2 = ⁰ 5) 1 1/Зх ² = 0 5) -10х2 = ⁰
а) 0; 2,7 а) 0; -0.07 а) 1 1/3 а) 0
б) -2,7 б) 0.07 6) 0 6) -10
в) 2,7 в) 0 в) 0; 1 1/3 в) -10;
г) 0 г) -0.07 г) -1 1/3 г) 10

👉ІІ. Письмове.
Звести рівняння до загального вигляду ах ² + вх + с = 0 .

АТ 1	АТ 2	АТ 3	АТ 4

1) (х-4) (х +11) = 0	1) (х-1) (х-9) = 0	1) (х+3)(х-4)=0	1) (х +5) (х-7) = 0
а) 4; 11	а) 1; -9	а) -3; -4	а) -5; -7
б) -4;-11	б) -1; 9	б) 3; -4	6) 5; 7
в) 4;-11	в 1 ; -9	в) -3; 4	в) 5; -7
г) -4; 11	г) 1; 9	г) 3; 4	г) -5; 7

2) х(х+0,5)=0	2) (х-0.1) х = 0	2) х(х-0.3)=0	2) (х +0.7) х = 0
а) 0; -0.5	а) 0.1	а) 0; 0.3	а) 0
6) 0	6) 0.1; 0	6) 0.3	6) -0.7; 0
в) -0.5	в) 0	в) 0; -0.3	в) 0; 0.7
г) 0; 0.5	г) -0.1;	г) 0	г) -0.7

3) х ² -2х = 0 '	3) х ² +Зх = 0	3) х ² - 5х = 0	3) х ² +7х = 0
а) 0; -2	а) 0; 3	а) -5	а) 0
6) 0	6) 0	6) 0; -5	6) 0; 7
в) 0; 2	у 3	в) 0; 5	о 7
г) 2	г) 0; -3	г) 0	г) 0; -7

4) 9х2-1 ⁼ 0	4) 16х2 ^-9 = 0	4) 25х2-4 ⁼ 0	4) 4х2-1 ⁼ 0
а) -1/3; 1/3	а) 9/16	а) 6 1/4	а) -2; 2
6) 1/9	б) -3/4; 3/4	6) -4/25; 4/25	6) нема розв'язку
в) нема розв'язку	в) -11/2; 11/2	в) -2/5; 2/5	в) 4/9
г) -3; 3	г) нема розв'язку	г) нема розв'язку	г) -1/2; 1/2

5) 2,7 х ² =0	5) -0.07х2 = ⁰	5) 1 1/Зх ² = 0	5) -10х2 = ⁰
а) 0; 2,7	а) 0; -0.07	а) 1 1/3	а) 0
б) -2,7	б) 0.07	6) 0	6) -10
в) 2,7	в) 0	в) 0; 1 1/3	в) -10;
г) 0	г) -0.07	г) -1 1/3	г) 10

1. Знайти D та вказати кількість коренів.
В 1 1) 5х2-4х- ¹ =0 2) 4х2 ⁼ 4х-1 3) -Зх-1 = ^6х2
В 2 1) Зх ² +2х-6 = 0 2) 9х ² = 6х-1 3) -4х-7 = 5х ²
2. Розв'язати рівняння (У №1, У №2)
У №1 У №2 У №3 У №4
1) 7х ² +8х +1 = 0 1) 5х ^2-9х -2 = 0 1) 5х ² -8х +3 = 0 1) 2х ² -15х +7 = 0
2) 4х ² -30х-13 = 6х-90 2) 13у ² -18у-33=2у+4у+4 2) 3х ² -15х +21 = 45-2х ² -41х 2) 5х2 +11х = ^2х2-21х - ⁸⁰
3) (х +3) ² = 2х +6 3) 3 (х + 4) ² = 10х + 32 3) 31х +17 = 15 (х +1) ² 3) (3х +4) ² = 4 (х +3)
4) (6х-4) (х-4) = 7 (х ² -4х-12) 4)(2у+7)(7-2у)+6у ² =49+7у 4) (Зх-4.5) (х-2) = х ² -2.5х +9 4) (1 + 5х) (5х-1) - 10 (х-2) = 19
Додатково Додатково Додатково Додатково
5) 2х ² +х/5=4х-2/3 5) х ² +Зх/2=х+7/4 5) х ² +х/2=8х-7/3 5) х ² -Зх/7 + х = 11

В 1	1) 5х2-4х- ¹ =0	2) 4х2 ⁼ 4х-1	3) -Зх-1 = ^6х2
В 2	1) Зх ² +2х-6 = 0	2) 9х ² = 6х-1	3) -4х-7 = 5х ²

У №1	У №2	У №3	У №4
1) 7х ² +8х +1 = 0	1) 5х ^2-9х -2 = 0	1) 5х ² -8х +3 = 0	1) 2х ² -15х +7 = 0
2) 4х ² -30х-13 = 6х-90	2) 13у ² -18у-33=2у+4у+4	2) 3х ² -15х +21 = 45-2х ² -41х	2) 5х2 +11х = ^2х2-21х - ⁸⁰
3) (х +3) ² = 2х +6	3) 3 (х + 4) ² = 10х + 32	3) 31х +17 = 15 (х +1) ²	3) (3х +4) ² = 4 (х +3)
4) (6х-4) (х-4) = 7 (х ² -4х-12)	4)(2у+7)(7-2у)+6у ² =49+7у	4) (Зх-4.5) (х-2) = х ² -2.5х +9	4) (1 + 5х) (5х-1) - 10 (х-2) = 19
Додатково	Додатково	Додатково	Додатково
5) 2х ² +х/5=4х-2/3	5) х ² +Зх/2=х+7/4	5) х ² +х/2=8х-7/3	5) х ² -Зх/7 + х = 11

Зразок.

Зведемо рівняння до загального вигляду ах ² + вх + с = 0 .

2) 4х ² -30х-13 = 6х-90;

4х2-30х - ^13-6х +90=0;

^4х2 -36х +77 = 0;

Якщо D = 1296-4 * 4 * 77 = 1296-1232 = 64; √64=8, то

Х1 = 11/2 = 5,5; Х2 = 7/2 = 3,5.

Відповідь. 5,5; 3,5.

👉ІІІ. Підсумок уроку
1) Як називаються дані рівняння:
а) 5х ² -6х+1=0
б) х ² -7х+5=0
в) 5х ² -1=0?
2) Які рівняння ми розв'язували на уроці?
3) За допомогою чого ми змогли їх розв'язати?
4) Якщо D = 0, то ...
Якщо D> 0, то ...
Якщо D <0, то ...

Неповне квадратне рівняння
ax ² + bx = 0
Розв'язок
ax ² + c = 0
Розв'язок
ax 2 = 0
Розв'язок
x = 0

ax ² + bx = 0 Розв'язок	ax ² + c = 0 Розв'язок	ax 2 = 0 Розв'язок x = 0

👉ІУ. Домашнє завдання.

Розв'язати рівняння (У №3, У №4). Повторити п.19, приклад 2, приклад 3 (с.148-151).

Геометрія

Урок 01.04.22.

Тема: "Поняття площі. Площа прямокутника".

👉І. Усно.

1. Повторити.

Одиниці вимірювання площ; ознаки рівності трикутників; властивості паралелограмів; означення і властивості прямокутника і квадрата та формули периметрів цих чотирикутників.

2. Під час вимірювання площ земельних ділянок використовують різні одиниці вимірювання. Що означає гектар; ар?

3. Що означає «сотка» місту?

4. Чи одне й те саме означають арі сотка?

5. ABCD - паралелограм (рис. 1). Доведіть, що ЗМ = ОК .

6. ABCD - паралелограм (рис. 2). Докажіть, що ΔABC = ΔCDA.
7. ABCD — прямокутник, ∠1 = ∠2 , ∠3 = ∠4 (рис. 3). Доведіть, що ВК = СМ.
8. Чи правильні твердження?
1) Шкірний квадрат є прямокутником.
2) Існує ромб, який є прямокутником.
3) Жодний прямокутник не є ромбом.

👉ІІ. Вивчення нового матеріалу.

1. Підручник с.152-154.

2. Конспект
Площа. Властивості площ. Площа прямокутника
Для площі S багатокутника М справедливо, що:
1) S> 0.
2) Якщо M розбити на частини із площами S1 і S2, то S = S1 + S2.
3) Одиниця вимірювання площі в одиничних квадратах: 1 мм2 1 см2 і т.д.
4) Якщо M1 = М2, то S1 = S2.
5) Якщо S1 = S2, то M1 і M2 — рівновеликі.
6) На рис. а, б, у фігури є рівноскладеними.


Багатокутники, складені з однакової кількості відповідно рівних багатокутників, називаються рівноскладеними.

Площа прямокутника

1) Теорема (про площу прямокутника) (с.153).

Для ABCD - прямокутника АВ = а, ВС = b, S = ab.

2) Наслідок. Для ABCD – квадрата (АВ = а) S = a2.

3) Наслідок. Площа прямокутного трекутника з катетами а і дорівнює половині добутків катетів: S = 1/2 аb (с. 153).

4) Завдання. S1: S2 = k2 (с.154).

3. "Пригадайте головне" 1-6, с.155.

👉ІІІ. Письмове.

1. Визначте площа квадрата, описаного навколо колу, радіус якого R.
2. Квадрат і прямокутник мають рівні площі. Сторона квадрата дорівнює 12, а одна зі сторін прямокутника — 9. Чому дорівнює друга сторона прямокутника?
4. Знайдіть площу прямокутника ABCD, якщо.
а) АВ = 9 см, ПС = 4 см;
б) АВ: ПС = 5: 1, P ABCD = 48 см;
в) AD = 12 див, АС = 13 див.
5. Діагональ квадрата дорівнює 12√2 м. Знайдіть площу квадрата.
6. Площа прямокутника дорівнює 128 см2. Знайдіть сторони прямокутника, якщо одна з них вдвічі більша за іншу.
7. Бісектриса угла прямокутника ділити його сторону на відрізки завдовжки 3 см і 4 см. Знайдіть площу прямокутника. Скільки розв'язків має завдання?

3. Периметр квадрата дорівнює 32. Чому дорівнює площа цього квадрата?

8. Підручник: №1012, №1016, №1024.

👉ІУ. Оціни собі: 😊; 😐; 😓.

Алгебра

Урок 29.03.22.

Тема: "Формулі коренів квадратного рівняння".

👉І. Усно.

1. Подайте у вигляді квадрата двочлена:
1) у ² – 16у + 64; 2) х ² + 6х + 9; 3) 2а + а ² + 1.
2. Фронтальне опитування:
1) Що таке рівняння? Наведіть приклади.
2) Що означає роз'язати рівняння?
3) Що таке корінь рівняння?
4) Яке рівняння називають квадратним?
5) Як називають числа а, b, с ?
6) Чому коефіцієнт а не може дорівнювати нулю?
7) Які існують квадратні рівняння?

👉ІІ. Вивчення нової теми.

Розв'яжемо рівняння 3х ² – 5х + 2 = 0 (квадратне рівняння загального вигляду, в якому виділення повного квадрату ускладнене).
Аналіз ситуації, що склалася, призводить до формування проблеми: "Необхідно знайти єдиний досить простий алгоритм вирішення квадратних рівнянь загального вигляду». Вирішення цієї проблеми є головною метою уроку.

2) Підручник п.19 (с.148-149). Прочитати.

3) написати конспект. Вивчити формули.

У квадратному рівнянні ах ² + bx + c = 0
D = b ² – 4ас – дискримінант, який показує кількість коренів.
1. Якщо D > 0, то квадратне рівняння має два різні дійсні корені х _1,2 = (- b ± √D) / 2 a (с.149 формула).
2. Якщо D = 0, то квадратне рівняння має два співпадаючі дійсні корені х = - b / 2a .
3. Якщо D < 0, то квадратне рівняння не має дійсних коренів.
Це формула коренів квадратного рівняння ах ² + bx + c = 0. Користуючись нею, можна вирішити будь-яке квадратне рівняння.

Роз'яжемо рівняння: 3х ² – 5х + 2 = 0.

а = 3, b = -5, с = 2, D = b ² - 4ас, D = (-5) ² - 4 • 3 • 2 = 25 – 24 = 1- більше 0,

х _1,2 = (- b ± √D) / 2 a,

х ₁ = (5 + 1) / 6 = 1, х ₂ = (5 – 1) / 6 = 4/6 = 2/3.
Відповідь: 2/3; 1.

☝Таким чином отримаємо АЛГОРИТМ розв'язання квадратного рівняння:
1. Виділити у квадратному рівнянні коефіцієнти.
2. Обчислити дискримінант D.
3. Якщо D<0, то рівняння не має дійсних коренів.
Якщо D > або = 0, то вирахувати корені за формулою:

х _1,2 = (- b ± √D) / 2 a

👉ІІІ. Письмове. п.19, с.150, приклад 1. Записати у робочу тетрадь розв'язки п'яти рівнянь.

👉ІУ. Розв'язати самостійно. Підручник: п.19 (с.148-150) №635 (непарні).

👉У. Оціни собі: 😊; 😐; 😓.

Геометрія

Урок 25.03.22.

Тема: "Багатокутник та його властивості. Вписань та опис багатокутників"

👉І. Усно.

Вивчення нової теми.

1. Підручник п.20, с.146-147.

1) Що таке багатокутник; n-кутник? Як його позначають? Сторони, куті, вершини багатокутника (рис.437).

2) Який відрізок називають діагональю багатокутника? (Рис.440).

3) Периметр багатокутника - сума довжин усіх його сторін (Р).

4) Теорема про суму кутів n-кутника. Формула обчислення: 180 (n – 2), де n – кількість сторін.

5) Що таке зовнішній кут багатокутника? (Рис.443).

6) Багатокутник, вписаний у коло (рис.444).

7) Багатокутник, опис навколо колу (рис.445).

2. Відповісти на запитання 1-6 с.148.

3. Виконайте управи: №946-953 (усно), №954, №956, №957, №960, №965 (листово).

👉ІІ. Оціни собі: 😊; 😐; 😓.

Алгебра

Урок 21.03.22.

Тема: "Квадратні рівняння. Неповні квадратні рівняння"

👉І. Усно.

Вивчення нової теми.

1. Підручник п.18, с.141-143, таблиця с.143.

2. Відповісти на запитання 1-8 с.143.

👉ІІ. Письмове.

1) Роз'яжемо наступні рівняння:

3х2 = ⁰ ; 2х ² - 18 = 0; -5х ² + 10х = 0
(неповні квадратні рівняння)
та х ² – 4х + 4 = 0; 25х2 +10х+1=0   ⁽
квадратні рівняння загального вигляду, у яких повний квадрат двочлена виділяється легко).
а) 3х2 = ⁰ ; х ² = 0; х = 0. Відповідь. 0.
б) 2х ² - 18 = 0; х ² – 9 = 0;  х ² = 9; х1 = √9 = 3; х2 = -√9 = -3. Відповідь. 3 і -3.
в) -5х2 + 10х = 0   ^;-5х (х – 2) = 0; х = 0 або х – 2 = 0; х = 2. Відповідь. 0 і 2.
г) х ² – 4х + 4 = 0; ( х - 2) ² = 0; х – 2 = 0; х = 2. Відповідь. 2.
д) 25х2 + 10х + 1 = 0 ^;( 5х + 1) ² = 0; 5х + 1 = 0; 5х = -1; х = -1/5. Відповідь. -1/5.
2. Розв'яжіть за взірцем: №589.
Приклад 1) зразок а); приклади 2), 4), 6) зразок б); приклади 3), 5), 7) зразок в); приклади 8), 9) зразок г), д).

👉ІІІ. Оціни собі: 😊; 😐; 😓.

Онлайн урок 17.11.21

Тема: "Розв'язання раціональних рівнянь"
👉І. Усно.

1. Обчисліть: ; ; ; ; ; ; ; 2. Вкажіть допустимі значення змінної у виразі: х2 – 4; ; ; ; ; . При яких значеннях змінних вирази набувають значення, що дорівнює нулю? 3. Назвіть порядок виконання дій у виразі:

👉ІІ. Письмове.
1. Заповніть таблицю:

Рівняння	ОДЗ	Значення змінної, при якій у чисельнику нуль	Не входити до ОДЗ	Відповідь


	х ≠ 5
	х ≠ 0, х ≠ -5	0; 5

2. У якому з випадків правильно розв'язане рівняння?

1) , х – 2 = 0, х = 2. Відповідь. 2
2) , 3) а) ОДЗ: х + 3 ≠ 0, х ≠ -3.
х + 3 = 0, х = -3.
б) х – 2 = 0, х = 2 – задовольняє ОДЗ.
Відповідь. -3
Відповідь. 2

3. Повторити п.7, приклади 1-3 №208 (2, 4, 6).

👉ІІІ. Домашнє завдання. Повторити п.7. Приклади 1; 2; 3. Письмове №208 (2, 4, 6).

Геометрія

Он-лайн урок 15.11.21

Тема: "Середня лінія трекутника та її властивості"

👉І. Усно.

Повторити п.6(1). "Пригадайте головне" с.40 №257 №260.

👉ІІ. Вивчення нового матеріалу.

1. Підручник. Вівчіті п.6 (2), с.39.
2. Конспект.

Визначення. Середньою лінією трекутника називають відрізок, який сполучає середини двох його сторін.
На малюнку 105 KL – середня лінія трекутника ABC.

Т е о р е м а 1 (властивість середньої лінії трекутника). Середня лінія трекутника, що сполучає середини двох сторін, паралельна третій стороні і дорівнює її половині.

Д о в д е н ня. Нехай KL – середня лінія трекутника ABC (рис. 105). Доведемо, що KL || AB і KL = 1/2 AB.
1) Проведемо через точку L пряму, паралельну AB. За теоремою Фалеса вона перетинає сторону AC у її середині, тобто в точці K. Отже, ця пряма містить середню лінію KL. Тому KL | AB.
2) Проведемо через точку L пряму, паралельну AC, яка перетинає AB у точці M. Тоді AM = MB (за теоремою Фалеса).
Чотирикутник AKLM – паралелограм. KL. = AM (за властивістю паралелограма), але AM = 1/2 AB. Тому KL = 1/2 AB

Малий. 105

Малий. 106
Завдання. Доведіть, що середини сторін чотирикутника є вершинами паралелограма, один з кутів якого дорівнює куту між діагоналями чотирикутника.

Д о в д е н ня. Нехай ABCD - даний чотирикутник, а точки K, L, M, N - середини його сторін (мал. 106).
KL – середня лінія трекутника ABC, тому KL || AC та KL = 1/2AC. Аналогічно MN | AC, MN = 1/2AC.
Отже, KL | MN, KL = MN. Тоді KLMN – паралелограм (за ознакою паралелограма).
KN – середня лінія трекутника ABD. Тому KN || BD. Отже, KFOP - також паралелограм, звідки: ∠NKL = ∠BOA.
Розглянемо властивість медіан трикутника.
Т е о р е м а 2 (властивість медіан трекутника). Медіані трекутника перетинаються в одній точці, яка ділить кожну з них у відношенні 2 : 1, починаючи від вершини трекутника.
Точку перетину медіан ще називають центром мас трекутника, або центроїдом трекутника.

Малий. 107
3. Усно №258, №259.
4. Письмове №268, №270, №271.

👉ІУ. Домашнє завдання. Вівчіті п.6 (2), с.39. Письмове №269, №272, №275.

Алгебра

Онлайн урок 15.11.21

Тема: "Рівносильні рівняння. Раціональні рівняння"
👉І. Усно.

Виконайте дії:

; ; ; ; ; ; ; .

👉ІІ. Письмове.
Конспект. 1. Рівносильними називають рівняння, які мають однакові корені.

2. Дробово-раціональне рівняння.
ОДЗ: значення змінної, за яких існують вирази в обох частинах рівняння.
3. Алгоритм розв'язання рівнянь виду А/В = 0 (А і В — багаточлен від однієї змінної).
А/В = 0.
1) В ≠ 0 (знайти ОДЗ рівняння):
2) А = 0 (знайти, при яких значеннях змінної чисельник дорівнює нулю);
3) (знайти, які з коренів рівняння А = 0 задовольняють ОДЗ рівняння); 4) Відповідь. (Запишіть у відповідь ці корені)

4. Основні прийоми розв'язання рівнянь:
1) заміна одного виразу іншим, рівним йому:
2) перенесення доданків з однієї частини рівняння на іншу зі зміною знака, на протилежний:
3) множення та ділення обох частин рівняння на один і той самий вираз (але нове рівняння може бути рівносильним з попереднім).

5. Розв'язування вправ.

№205. Чи є рівносильними рівняння?

1) х + 2 = 10 і 3х = 24

х = 10 - 2 х = 24: 3

х = 8 х = 8.

Рівняння рівносильні.
Рівносильні.
Нерівносильні.

Дані рівняння рівносильні.
Обидва рівняння не мають коренів, тому вони рівносильні;
Для обох рівнянь будь-яке число є коренем, тому рівняння є рівносильними.

6. У якому з випадків правильно розв'язане рівняння?

а) ;
(2х – 3)(х – 1) = (2х – 1)(х + 3),
2х2 + 3 = 2х2 – 3, 3 = -3 – коренів немає

б) .
1) ОДЗ: 2х - 1 ≠ 0 та х - 1 ≠ 0; х ≠ та х ≠ 1;
2) (2х - 3) (х - 1) = (2х - 1) (х + 3),
2х2 - 3х - 2х + 3 = 2х2 - х + 6х - 3,
- 5х + 3 = 5х - 3,
- 10х = -6,
х = 0,6 - задовольняє ОДЗ.
3) Відповідь. 0,6

7. Листове №207 (7; 9; 11).
👉ІІІ. Домашнє завдання. Вивчіті п.7. Приклади 1; 2; 3. Листове №208 (непарні).

Онлайн урок 08.11.21

Тема: "Тотожні перетворення раціональних виразів"
👉І. Усно.

1. Яка послідовність дій у виразі ?
2. Прокоментуйте виконання дій у виразі .
1) ; 2) ; 3) .
Відповідь. .
3. Розкладіть на множники вираз:
а) mn - nk; б) m2n - mk; в) 9m2n - 6mk; г) m2 – n2; д) m2 – 1;
є) m2 – 4n2; ж) m3 – 4m; з) m3 + 8; і) m4 - 4m3 + 4m2.

👉ІІ. Письмове.

Тотожні перетворення раціональних виразів

1. Перетворення будь-якого раціонального виразу можна звести до додавання, віднімання, множення та ділення раціональних дробів.

Які з рівностей є тотожностями. Чому?

а) ; б) ; в) ; г) ?

2. Суму, різницю, добуток і долю раціональних дробів завжди можна подати у вигляді раціонального дробу.

Подайте вираз у вигляді дробу: а)

; б)

; в)

; г)

; д)

; є)

; ж)

; з)

3. Будь-який раціональний вираз можна подати у вигляді раціонального дробу.

1) Спростіть вираз:

а) ; б) ; в) ;

г) .

👉ІІІ. Домашнє завдання. Повторити п.6 №183 №181 (3; 4).

Геометрія

Он-лайн урок 09.11.21

Тема: "Теорема Фалеса"

👉І. Усно.

Повторити п.8, 9. (Урок 05.11.21).

👉 ІІ. Натисніть на постлання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSd8BZGs2iqLIH2BEwCI_NSjLTq_6qm9hhMlAfQT-NYVJkyxXA/viewform?usp=sf_link

👉ІІІ. Вивчення нового матеріалу.

1. Підручник п.6(1), с.38.
а) Теорема Фалеса.
б) Завдання. Поділити на 5 рівних частин даний відрізок АВ (рис.120).

2. Усно №257, №260, №261.

3. Письмове №262, №264 (1), №266.

👉ІУ. Домашнє завдання. Вівчіті п.6 (1), с.38. Письмове №263, №265.

Алгебра

Урок 08.11.21

Тема: "Тотожні перетворення раціональних виразів"
І. Усно.

Повторити додавання раціональних дробів.

👉ІІ. Вивчення нового матеріалу.

1. Конспект.

Тотожні перетворення раціональних виразів

1. Перетворення будь-якого раціонального виразу можна звести до додавання, віднімання, множення та ділення раціональних дробів.
2. Суму, різницю, добуток і долю раціональних дробів завжди можна подати у вигляді раціонального дробу.
3. Будь-який раціональний вираз можна подати у вигляді раціонального дробу. Для цього:
а) встановлюємо (визначаємо), які дії з раціональними дробами слід виконати, виходячи з умови завдання;
б) виконуємо ці дії або в порядку спадання дії, або користуючись законами (владами) арифметичних дій (перестановка + і; сполучна + і; розподільна) та властивостями раціональних дробів (основною властивістю дробу)

2. Підручник п.6, с.3840. Приклади1; 2; 3.
3. Письмове.

Приклад 1.

Виконай дії:

x−y6y÷x2−y2y⋅x2+2xy+y2x.

Спрощення виконується у дві дії: спочатку ділення, а потім множення. Чисельники та знаменники розкладаються на множники у кожній дії.

Приклад 2.
Довести тотожність: перетворимо праву та ліву частини.

a+b2(a−b)−a−b2(a+b)=ba−b−b2−aba2−b2

У першій та другій частинах ми отримали однаковий вираз:

2aba2−b2=2aba2−b2

Це означає, що тотожність доведена.
Під час доведення були застосовані формули скороченого множення:

a2−b2=(a−b)(a+b)(a+b)2=a2+2ab+b2(a−b)2=a2−2ab+b2

4. №176 (1; 3; 5; 7)
👉ІІІ. Домашнє завдання. Вівчіті п.6, с.38-40, №177 (1; 3; 5; 7).

Геометрія

Урок 05.11.21

Тема: "Вписані і центральні куті. Вписані і описані чотирикутники. Розв'язання задач".

👉І. Усно.

Який угол називається центральним?
Що вважають градусною мірою дуги колу?
Що таке кут, вписаний у коло?
Як вимірюється вписаний кут?
Сформулюйте наслідки з теореми для вписань кут.
Який чотирикутник називається вписаним у коло?
Який чотирикутник називається описаним навколо кола?
Сформулюйте властивість кутів вписаного чотирикутника.
Сформулюйте властивості сторін описаного чотирикутника.
Сформулюйте ознаку вписаного чотирикутника, описаного чотирикутника.
Натисніть на посилання . Продивіться відео (теоретичний матеріал)

https://youtu.be/9HebHj-txe0

Виконання усних вправ

1. Чи можна описати коло навколо прямокутної трапеції

2. У трапеції три сторони рівні. Чи можна в таку трапецію вписати коло? Чи можна навколо такої трапеції описати коло?

👉ІІ. Виконання письмових вправ.

До задач накресліть малюнки.

1. Визначте, чи можна описати коло навколо чотирикутника ABCD, якщо кути А, В, С, D дорівнюють відповідно:

а) 90 °, 90 °, 20 °, 160 °; б) 5 °, 120 °, 175 °, 60 °.

Розв'язання. Якщо в чотирикутнику сума двох протилежних кутів дорівнює 180 градусів, то навколо чотирикутника можна описати коло:

а) 90 ° + 20 ° = 110; 90° +160°=250 , то навколо чотирикутника не можна описати коло.
б) 5 ° + 175 ° = 180; 120° + 60° =180 градусів, то описати можна.

2. Знайдіть невідомі кути:

а) вписаного чотирикутника, якщо два з них дорівнюють 46° та 125° .

Розв'язання. Якщо чотирикутник вписань, то суми протилежних кутів 180 градусів і 180-46 = 134; 180-125 = 55.

б) вписаної трапеції, якщо один із них дорівнює 80°.

Розв'язання. якщо трапеція вписана у коло, то вона рівнобічна. Кути, прилеглі до бокової сторони трапеції, у сумі складають 180 градусів. Маємо 180-80=100 градусів.

в) вписаного чотирикутника, діагоналі якого точкою перетину діляться навпіл.

Розв'язання. Якщо діагоналі точкою перетину діляться напіл, то чотирикутник - паралелограм. Якщо навколо паралелограма описано коло, то він прямокутник. Усі куті по 90 градусів.

3. Знайдіть периметр:

а) описаного чотирикутника, три послідовні сторони якого дорівнюють 7 см, 9 см і 8 см

Розв'язання. Якщо в чотирикутнику суми протилежних сторін рівні, то цей чотирикутник можна вписати коло, отже 7+8=9+х, х=15-9=6; Р=7+9+8+6=30 см

б) описаної трапеції, бічні сторони якої дорівнюють 3 см і 11 см

Розв'язання. Якщо трапеція описана, то коло вписане у трапецію. Тоді суми протилежних сторін рівні. Маємо: (3+11)*2=28 см = Р трапеції.

4. Рівнобедрена трапеція описана навколо колу. Знайдіть середню лінію трапеції, якщо її бічна сторона дорівнює 7 см .

Розв'язання. Якщо в трапецію вписано коло, то суми протилежних сторін рівні. Сума основ дорівнює сумі бічних сторін. Середня лінія трапеції дорівнює півсумі основ, маємо (7+7) : 2=7 см

5. Діагональ ромба, що виходить з вершини угла 60°, дорівнює 24 см. Знайдіть радіус колу, вписаного в ромб.

Розв'язання. Якщо в ромб вписано коло, то його радіус дорівнює половині висоти ромба. Діагональ ромба, що лежить проти кута 60 градусів, ділить ромб на два рівносторонні трекутники. Діагональ ромба, що виходить з вершини угла 60 градусів, 24 см. Половина діагоналі є висотою рівностороннього трекутника. Тоді R=12:2=6 см - радіус вписаного біля ромба колу.

👉ІІІ. Домашнє завдання. Повторити п.8, 9, с.52-61. Відповісти на запитання "Пригадайте головне" 1-5, с.55; 1-4, с.62. Письмово тестові завдання №3 (1-5), с.67.

Алгебра

Урок 03.11.21
Тема: "Ділення раціональних дробів. Тест-контроль"

👉І. Усно.

1. Підручник. Повторити п.5, с.32-34.
👉ІІ. Письмове.
Завдання №2 (1-7) "Перевір собі" у тестовій формі, с.44-45.

👉ІІІ. Домашнє завдання. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSdgYn_xabYtaA9yrRXdIHGD_2y4InxJ4u7tq6d4r7pJIiGi9Q/viewform?usp=sf_link

Геометрія

Урок 02.11.21
Тема: "Вписані та описані чотирикутники"
👉І. Усно.

Виконання усних вправ за готовими малюнками.

☝Увага! Дотічна, перпендикулярна до радіусу колу, опущеного в точку з'єднання.

1		Дано: ВС – дотична, О – центр колу, АВ = АС. Довести: ОВ = ОС
2		Дано: О - центр колу, 1 = 45 °. Знайти: кут 2
3		Дано: МН - дотична, ∠1 = ∠2. Довести: АВ = АС

👉ІІ. Вивчення нового матеріалу. Підручник п. 9, с.59-61.
1. Означення чотирикутника, вписаного в коло.
2. Теорема для записів чотирикутник.
3. Наслідки з теореми для вписань чотирикутників.
4. Означення описаною чотирикутника.
5. Теорема для описів чотирикутник.
6. Наслідки з теореми для описів чотирикутник.
На якому із наведених малюнків зображено чотирикутник ABCD:
а) вписань у коло;
б) описів навколо кола?

☝Запам'ятати.
1. Центр колу описаного навколо прямокутника є точкою перетину його діагоналей.
2. Центр колу, вписаного в ромб, є точкою перетину його діагоналей, а радіус колу дорівнює половині висоти ромба.
3. Радіус колу, вписаного в трапецію, дорівнює половині її висоти.

Конспект 10
Вписань і опис багатокутники (вписані і описані кола)
О - центр колу, R - радіус колу
Вписань — всі вершини лежати на колі
Описів - усі сторони є дотичними до колу.
Вписань та описів чотирикутники
Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює 180 градусів
∠A + ∠C = 180 градусів,
∠B + ∠ D = 180 градусів
І навпаки: якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло
AB + CD = BC + AD
(суми довжин протилежних сторін рівні)
І навпаки: якщо суми довжин протилежних сторін випуклого чотирикутника рівні, то в нього можна вписати коло
Прямокутник
R – радіус колу, О – центр колу, d – діагональ прямокутника.
R = 1/2 d
1. Якщо паралелограм вписано в коло, то він прямокутник.
2. Центр колу, описаного навколо прямокутника, - точка перетину діагоналей
Трапеція та ромб
Якщо ABCD – вписана трапеція, то AB = CD
d впис. коли = h
O — точка перетину бісектрис внутрішніх кутів.
ㄥAOB = ∠ COD = 90°
Квадрат
а - сторона квадрата
О - центр колу
d - діагональ квадрата

R - радіус описаного колу
R = 1/2 d

👉ІІ. Письмове. Підручник №431, №438.

👉ІІІ. Домашнє завдання. Вівчіті п.9 №433 №439.

Алгебра

Урок 01.11.21

Тема: "Ділення раціональних дробів"
👉І. Усно.

1. Повторити правила.

Конспект
Множення і піднесення до ступеня раціональних дробів
	1. Для будь-яких А, В, С і D де В ≠ 0, D≠0, справджується равенство:

	2. Для будь-яких А і В, В ≠ 0, справджується рівність:

👉ІІ. Вивчення нового матеріалу.

1. Конспект. Ділення раціональних дробів.

Для будь-яких А, В, С і D де B ≠ 0, C ≠ 0, D ≠ 0, справджується рівність:
Зауваження. Дріб, яким записується добуток або частка дробів необхідно (якщо це можливо) скоротити! Записувати його раціональним дробом — тільки виходячи з умови завдання

2. Підручник.

1) Вівчіті п.5, с.33 Правило.

2) Приклад 1 (3; 4), приклад 2, с.33.

3) Усно №148.

4) Письмове №149, №151 непарні.

👉ІІІ. Домашнє завдання. Вівчіті п.5, №150, №152.

Урок 29.10.21

Тета: "Піднесення дробу до ступеня"

І. Усно.

1. Обчисліть: ; ; ; ; ; .
2. Подайте у вигляді степеня з основою у виразі:

у ∙ у3; у10 ∙ у2; ; ; у18 ∙ у2; ; .

3. Розкладіть вираз на множники:

а) ах – а; б) х2 + 1 - 2х;

в) х2 + 8х; г) 2у2 - 8;

д) у3 - x2y;

е) k3 – x3;

ж) 4х2+16х+16;

з) 27 + 3у2 - 18у.

4. Яких значень (рівних чи протилежних) набувають при одному й тому самому значенні змінної вирази:
а) – х і х; б) х – 2 та 2 – х; в) і .

👉ІІ. Вивчення нового матеріалу.

Конспект
Множення і ділення раціональних дробів
	1. Для будь-яких А, В, С і D де В ≠ 0, D ≠ 0, справджується рівність:

	2. Для будь-яких А і В, В ≠ 0, справджується рівність:

1. Підручник п.5, с.33-34 (починаючи зі слів: "Застосовуючи правило множення дробів...").

2. Приклад 3 (с.34).

3. Письмове №153, №158 (1; 2; 3).

👉ІІІ. Домашнє завдання. Вивчіти п.5 ( починаючи зі слів: "Застосовуючи правило множення дробів..."), №154, №156 (3), №159 (1; 2; 3).

Урок 27.10.21.

Тема: "Множення раціональних дробів"
👉І. Усно.

1. Подати у вигляді ступеня:
а ⁵ * а ^2;b ⁷ * b ³

2. Розкласти на множники:

1) mx – m

2) 14n ² – 14
3) m ² + n ² - 2mn

👉 ІІ. Вивчення нового матеріалу.

1. Натисніть на посилання. Продивіться відео.

https://youtu.be/AjDTZs9FZkQ

2. Підручник п.5, с.32-33, приклад 1 (1-2).

3. Усно №143.

4. Листове №144 (непарні), №146 (непарні).

👉ІІІ. Домашнє завдання. Вивчіті п.5 (правило 1, с.32), №145, №147.

Геометрія.

Урок 26.10.21.

Тема: "Вписані та центральні куті".

👉І. Усно.

1. Вівчіті п.8 (с.52).

1) Що таке центральний кут?
Градусна міра центрального угла дорівнює градусній мірі відповідної дуги колу.

Кут із вершиною в центрі кола називається центральним углом.

2) Що таке вписаний кут?

Кут, вершина якого лежить на колі, а сторони перетинають коло, називається вписаним углом.

3) Теорема (про вписання кут). Наслідок1. Наслідок 2.

1. Вписаний кут вимірюється половиною дуги, на яку він спирається.

2. Вписані кути, що спираються на одну й ту саму дугу, рівні.

3. Вписаний кут, що спирається на півколо, дорівнює

4) Завдання (с.54).

5) №373-№381 (с.55)

👉ІІ. Письмове.

1. Написати конспект п.8, використавши питання 1-5 "Пригадайте головне" (с.55).

2. Чому дорівнює центральний угол, якщо відповідний йому вписаний угол дорівнює 27,3 ° ?

3. Якщо кут CAB дорівнює 56 градусів то градусна міра дуги CnB дорівнює ...

4. Вирахуй угол ASB , якщо градусна міра дуги

ASB

дорівнює 248 градусів.

5. ∪ AB = 100, ∪ AC = 108,
Знайди угол ВОС BOC та кут ВАС.

6. Трикутник PR T - рівнобедрений,
- основа трекутника, дуга колу RT= 40 градусів.
Визначте куті трекутника: кут Р, кут R, кут Т. 7. Виконати №383, №388, №395.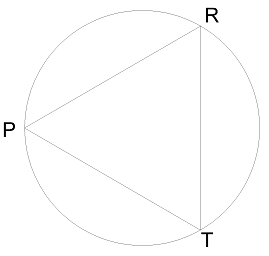

👉ІІІ. Домашнє завдання. Вівчіті п.8.

Алгебра

Урок 25.10.21.

Тема : "Основна властивість дробу. Додавання і віднімання дробів".

👉І. Усно.

Повторити п. 1-4. Урок 15.10.21.

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSeGxnWzghOk91Yl6tjfV5teaoVYMYCxhlCjezip9dQzTfK2DA/viewform?usp=sf_link

👉ІІІ. Домашнє завдання. Повторити п. 1-4.

Контрольна робота (письменно у робочих тетрадях)

1. При яких значеннях змінної Х вираз не має змісту?
(х+1)/(х-1) (знак / - ризику дробу).
2. Скоротіть дроб: (7а-14в) / (9а-18в)
3. Зведіть дроб 2у/3х до знаменника 45ху.
4. Виконайте додавання: 1) (3х/(х-2) - 6/(х-2); 2) у/7+(у-2)/8.
5. Знайдіть різницю: (а+3)/а2 – 1/а.
6. Виконайте дії:
3/(х+2) + (х+1)/(х2-9) + (х-1)/(х+3)(х+2).
7. Знайдіть суму дробів:
(5-а)/(а2-8а+16) і 6/(5а-20).
8. Спростіть вираз:
(4х-3)/(3-2х) – (4+5х)/(3-2х) – (3+х-10х2)/(4х2-9).
9. Доведіть тотожність:
1/(а-в)(а-с) – 1/(а-в)(в-с) + 1/(с-а)(с-в)=0

Урок 15.10.21

Тема: "Додування і віднімання дробів із різними знаменниками".

👉І. Усно.

1) Щоб додати або відібрати дроби, знаменниками яких є різні багаточлені, необхідно:
- Знайти спільний знаменник;
- звести дроби до спільного знаменника;
- виконати зазначені дії;
- якщо можливо, спростити результат.
2) Якщо знаменниками дробів є багаточлени, то спільним знаменником цих дробів також буде багаточлен, який знаходимо наступним чином:
- знаменники всіх дробів розкладаються на множники (якщо це необхідно та можливо);
- з одного знаменника беруться всі множники, а з інших тільки ті, яких немає у першому знаменнику (тобто ті, яких «бракує»).
3)Якщо багаточлени у знаменниках дробів неможливо розкласти на множники, то спільний знаменник таких дробів дорівнює видобутку знаменників усіх дробів.
Аби безпомилково визначити додатковий множник для шкірного дробу, отриманий спільний знаменник краще записати в знаменнику «нового» дробу.

👉ІІ. Письмове.
Зразок .

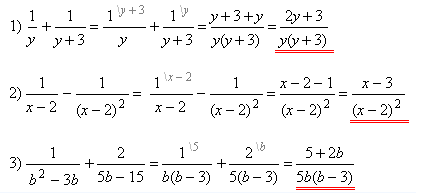
Приклад 4)
Алгоритм розв'язання.
1. Знаменники дробів розкладаємо на множники:
2. Знаходимо спільний знаменник.
У знаменника першого x(x–y) , на відміну від знаменника іншого дробу, не вистачає множника   y, тому спільним знаменником цих дробів є x(x−y)⋅y=xy(x−y). x(x−y) ⋅ y = xy (x−y) . 3. Зводимо дроби до спільного знаменника, додаємо їх та спрощуємо результат: 👉ІІІ. Виконати самостійно.

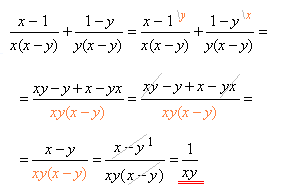
1) Виконайте дії
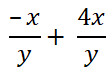
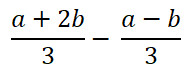
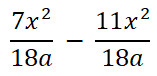
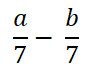
2) Виконайте дії 3) Виконайте дії 4) Виконайте дії 5) При яких значеннях змінної х вираз (Х+1)/(Х-2) не має змісту?  6) Зведіть дроб 2У/3Х до знаменника 15 𝑥𝑦 .

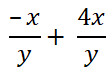
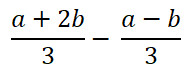
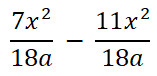
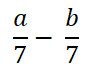
7) Виконайте додавання: У/4+(У-2)/5

8) Знайдіть різницю: (с-3)/2с - 1/с

👉ІУ. Домашнє завдання.

Повторити п. 1-4 №107 (1) №109 (2) №117 (1).

Урок 13.10.21.
Тема: "Додавання і віднімання дробів із різними знаменниками".
👉І. Усно.

1 . Які вирази називають раціональними? Які з наведених раціональних виразів цілі? Які дробові? 3а; ; 15р2q; ; ; .

2. Як додати (відняти) дроби з різними знаменниками? Розкажіть на прикладі дробів: а) і ; б) і (дивись приклад1 підручника (п.4, с.24-25)).

3. Як додати (відняти) раціональний дріб і цілий вираз? Покажіть це на прикладі виразів і а – b (дивись приклад 2 підручника (п.4, с.25)).

👉ІІ. Письмове.
1. Скоротіть дроби: а) ; б) ; в) .
2. Подайте у вигляді дробу вирази: а) ; б) ; в) ; г) ; д)
3. Спростіть вираз .
4. Знайдіть значення виразу: а) за а = ; х = ; б) за b=4; а = 3.
5. Доведіть, що при всіх допустимих значеннях вираз тотожно дорівнює нулю:

👉ІІІ. Домашнє завдання. Повторити п. 1-4 №73 (2,4) №76 (1,2) №101(парні) №105.

Геометрія

Урок 12.10.21.

Тема: "Узагальнення та систематизація знань з теми: "Чотирикутники". Тест-контроль".

👉Усно.

1. За даними рис. 1 знайдіть куті паралелограма ABCD. 2. За даними рис. 2 знайдіть периметр паралелограма АВСD На рис. 5 ABCD - прямокутник. Знайдіть куті х і у.

👉ІІ. Письмове.
1. На рис. 6 ABCD-ромб. Знайдіть куті х і у.
2.
Дано: ABCD - трапеція, AB = BC = CD = 5 см, СН丄AD,
ㄥDСН = 30 °.
Найти: AD
👉ІІІ. Натисніть на посилання. Пройдіть тест.
https://docs.google.com/forms/d/e/1FAIpQLSfyVB-v2jDEDWhZQc3iNVruQ1gApXivjeTae5oOklCmNGKnkA/viewform?usp=sf_link
👉ІУ. Домашня робота. Повторити п.1-5, с.31, п.7, с.44. Запитання 1-7, с.66. Розв'язати задачі.
1. Знайдіть кут паралелограма, якщо один з них на 36° менший від іншого.
2. ABCD - ромб (рис. 3 а, в). Визначте угол х.

Дистанційний урок №21: 26.04.21.

ZOOM. 13.00

Тема: "Площі багатокутників. Самостійна робота"

👉І. Усно.

1. Повторити уроки п.20-24, с.144-178.

👉ІІ. Письмово.

Самостійна робота.

1) Площа прямокутника дорівнює 27 см ² , одна з його сторін дорівнює 3 см. Знайдіть довжину другої сторони.
Варіанти відповідей.
30 см
9 см
24 см
12 см
24 см
2) Периметр квадрата дорвінює 32 см. Знайдіть площу квадрата, Вкажіть значення см 2 .
8
16
64
256
4
3) Знайдіть гіпотенузу прямокутного трекутника, якщо його площа дорівнює 40 см 2 , а висота, проведена з вершини прямого угла, дорівнює 8 см
10 см
5 см
20 см
15 см
інша відповідь
4) Сума кутів опуклого шестикутника дорівує .... Значення величини вкажіть у градусах.
360
540
720
1080
5) Площа трапеції з основами 4 см і 8 см та висотою 6 см дорівнює... Значення величини вкажіть у см 2 .
72
40
36
28
6) Площа паралелограма зі стороною 6 см та висотою, проведеною до неї, 5 см дорівнює... Значення величини вкажіть у см 2 .
60
15
30
11
1
7)Скільки діагоналей має опуклий п'ятикутник?
Варіанти відповідей
4
5
6
7
8
8)Обчисліть площу прямокутного трекутника з катетами 3 см і 4 см. Значення величини вкажіть у см 2 .
12
7
6
1
3,5
9)Обчіліть площу квадрата з діагональю 6 см. Значення величини вкажіть у см 2 .
36
18
12
24
10) Обчисліть площу прямокутника зі сторонами 5 см і 4 см. Значення величини вкажіть у см 2 .
9
18
20
10
8
11) Обчисліть площу трикутника зі стороною 6 см і висотою, проведеною до неї, 5 см. Значення величини вкажіть у см 2 .
30
11
15
60
1
12)Периметр ромба 20 см, а його висота - 5 см. Обчисліть площу ромба. Значення величини вкажіть см 2

👉Домашнє завдання. Задачі с.р. письмово.

Урок 1 (14.12.20)

Тема. "Подібність трикутників. Розв'язання задач."

І. Усно.

1. Повторити п.10-13, с.70-99.

Сформулювати умови, за яких ΔABCလ∆A 1 B 1 C 1:

1) за І ознакою ( ∠А= ∠А1, ∠В= ∠В1) за двома рівними кутами;

2) за ІІ ознакою ( ∠А= ∠А1, АВ/А1В1=АС/А1С1) за двома пропорційними сторонами та кутом між ними;

3) за ІІІ ознакою (АВ/А1В1=ВС/В1С1=АС/А1С1) за трьома пропорційними сторонами.

ІІ. Письмове.

Задача 1. Сторони одного трикутника дорівнюють

а) 3см, 6см та 7см; б) 5м, 35м і 30м,

а дві сторони подібного йому трикутника

а) 15см та 35см; б) 7м та 6м.

Обчисліть довжину третьої сторони.

Задача 2. 5. Визначте, чи подібні трикутники, якщо сторони:

а) 2см, 5см, 6см і 8см, 18см, 20см;

б) 5см, 8см, 9см і 15см, 24см, 27см.

Завдання 3. Знайти недосяжну відстань між домиками, якщо відстань від одного з них до лісу – 10 км, протяжність ділянки дороги, що проходити паралельно – 4км, а відстань від автобусної зупинки до лісу – 2 км.

Розв'язання:

Складемо математичну модель даного завдання. Накресліть малюнок.

1) ТрикутникиACB і DCE подібні (за двома кутами), так як DE паралельноAB, а AB та DE січні.

2) Значить AB=20 (м)

Відповідь: 20м

4. Контрольна робота 3. "Подібність трикутників".

(О.М.Роганін. Комплексний зошит для контролю знань. Геометрія 8. Стор.45, 1 варіант. Задачі 1-3, 5-7)

ІІІ. Домашнє завдання.

Контрольна робота 3. "Подібність трикутників".

(О.М.Роганін. Комплексний зошит для контролю знань. Геометрія 8. Стор.45, 2 варіант. Задачі 1-3, 5-7)

Алгебра.

Урок 1 (14.12.20)

Тема. "Властивості степеня з цілим відємним показником".

І. Усно.

1. Повторити п.8, с.53.

2. Відповісти на запитання.

1) добуток n множників, кажен з яких дорівнює а називається… (степенем);

2) число, яке підносимо до степеня називаемо… (основою);
3) число, в яке підносимо степінь називаємо… (показником);
4) яке число отримаємо при піднесені до степеня додатного числа? (додатнє);
5) яке число отримаємо при піднесені до степеня від’ємного числа в парну степінь? (додатнє);
6) яке число отримаємо при піднесені до степеня від’ємного числа в непарну степінь? (від’ємне);
7) чому дорівнює степінь а з показником 0? (один);
8) Щоб помножити степені з однаковими основами, потрібно….(основи залишити без змін, а показники додати);
9) Щоб поділити степені з однаковими основами, потрібно….….(основи залишити без змін, а показники відняти);
10) Щоб піднести степінь до степеня, потрібно….….(основи залишити без змін, а показники перемножити);
11) Щоб піднести дріб до степеня, потрібно….( окремо чисельник піднести до степеня, потім окремо знаменник піднести до степеня).
Кожна вірна відповідь 0,5 бал.

2. Вивчити п.9, с.61-64.

ІІ. Письмово.

1. Подайте вираз у вигляді степеня з основою а:

1 ). а :а³·а ³; 2). (a ) ³·a ¹²; 3). a ¹²·a ; 4). (a³) ²:а³; 5). а˚·a ³·a ;

6). (a ) ¹·a

2. Спростіть вираз:

1). 2 а ³b ·5а b ; 2). (0,1а ²b ¹) ¹; 3). 0,5 а ³ b · 2а b ² ;

4). 0,5 а³ b :(0,1а ² b ).

3. №275 (непарні), див. приклад 1 (с.62-63), №276 (непарні), див. приклад 2, №282(1,4),див приклад3(1), №286 (застосувати формули скороченого множення).

4. № 289 (застосувати формули скороченого множення, винесення за дужки спільного множення для розкладання многочлена на множники), №298 (1,2) (дивись приклад 3(2), стор. 63).

ІІІ. Домашнє завдання.

Повторити п.8, вивчити п.9, №275, №277, №283 (1,3), №287 (застосувати формули скороченого множення).

Завдання з дистанційного навчання з 19.10.20 по23.10.20

Алгебра.

Урок №2. 21.10.20.

Контрольна робота з теми:

"Основна властивість дробу. Додавання і віднімання дробів".

1. При яких значеннях змінної Х вираз не має змісту?
(х+1)/(х-1)
2. Скоротіть дріб: (7а-14в) / (9а-18в)
3. Зведіть дріб 2у/3х до знаменника 45ху.
4. Виконайте додавання: 1) (3х/(х-2) - 6/(х-2); 2) у/7 + (у-2)/8.
5. Знайдіть різницю: (а+3)/а2 - 1/а.
6. Виконайте дії:
3/(х+2) + (х+1)/(х2-9) + (х-1)/(х+3)(х+2).
7. Знайдіть суму дробів:
(5-а)/(а2-8а+16) і 6/(5а-20).
8. Спростіть вираз:
(4х-3)/(3-2х) - (4+5х)/(3-2х) - (3+х-10х2)/(4х2-9).
9. Доведіть тотожність:
1/(а-в)(а-с) - 1/(а-в)(в-с) + 1/(с-а)(с-в)=0

Геометрія

Урок №1. 19.10.20

Тема: "Узагальнення та систематизація знань з теми "Чотирикутники".

І. Усно.

1) Повторити: 1. п.1-5, п.7. (с.8-51).

2) Відповісти на контрольні запитання 1-7 (с. 66).

ІІ. Письмово.

1) Обчисли інші кути паралелограма, якщо кут C дорівнює 48 °

2) Один кут паралелограма в 2 разів більший від іншого. Обчисли кути паралелограма.

3) Умова:

ABCD - паралелограм, АС діагональ паралелограма.

∠BCA

= 32, ∠BAC = 20. Знайти кути ВАД, ВСД, В, Д.

4) Одна сторона паралелограма складає 27 см,

а друга — на 7

см

більша. Обчисли периметр паралелограма.

5) Обчисли тупий кут ромба, якщо одна діагональ зі стороною утворює кут величиною 25 ° .

6) Висота ромба зі стороною утворює угол завбільшки 15 °. Обчисли тупий угол даного ромба.

7) Маємо: АВСД – трапеція. ∠A = 77 ° , ∠C _ _= 121 °

Найди: ∠ B і ∠ D.

8) Обчисли інші кути трапеції A B CD , якщо ∠A = 41 ° _

ІІІ. Домашнє завдання.

Тестові завдання 1-5(с.66).

(Задачі 4-5 виконати письмово з повним обґрунтуванням)

Раціональний дріб
Квадрат числа	у = х2
Квадратний корінь	?

2. Конспект
Площа. Властивості площ. Площа прямокутника
Для площі S багатокутника М справедливо, що: 1) S> 0. 2) Якщо M розбити на частини із площами S1 і S2, то S = S1 + S2. 3) Одиниця вимірювання площі в одиничних квадратах: 1 мм2 1 см2 і т.д.
4) Якщо M1 = М2, то S1 = S2. 5) Якщо S1 = S2, то M1 і M2 — рівновеликі. 6) На рис. а, б, у фігури є рівноскладеними.

Шляхом рівносильних перетворень: дробово-раціональні рівняння:
	рівняння вигляду , де P(х) і Q(х) — багаточлени від однієї змінної, рівносильні системі:

Конспект 10
Вписань і опис багатокутники (вписані і описані кола)
	О - центр колу, R - радіус колу
Вписань — всі вершини лежати на колі	Описів - усі сторони є дотичними до колу.
Вписань та описів чотирикутники

Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює 180 градусів ∠A + ∠C = 180 градусів, ∠B + ∠ D = 180 градусів І навпаки: якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло	AB + CD = BC + AD (суми довжин протилежних сторін рівні) І навпаки: якщо суми довжин протилежних сторін випуклого чотирикутника рівні, то в нього можна вписати коло
Прямокутник
	R – радіус колу, О – центр колу, d – діагональ прямокутника. R = 1/2 d 1. Якщо паралелограм вписано в коло, то він прямокутник. 2. Центр колу, описаного навколо прямокутника, - точка перетину діагоналей
Трапеція та ромб

Якщо ABCD – вписана трапеція, то AB = CD	d впис. коли = h O — точка перетину бісектрис внутрішніх кутів. ㄥAOB = ∠ COD = 90°
Квадрат
	а - сторона квадрата О - центр колу d - діагональ квадрата
	R - радіус описаного колу R = 1/2 d

8 клас

Дистанційне навчання з 21.03.22.

Алгебра

Урок 01.06.22

Тема. "Підсумкова контрольна робота"

👉ІІ. Натисніть на посилання. Пройдіть тест.

Геометрія

Урок 31.05.22

Тема. "Підсумкова контрольна робота"

👉ІІ. Натисніть на посилання. Пройдіть тест.

https://docs.google.com/forms/d/e/1FAIpQLSeZ0_ki4bXiODYjPgoO9g2aB2s4zSjTKgh_VlLzNrbARZPDDA/viewform?usp=sf_link

(Тестові завдання виконати письмово у зошиті. Фото контрольної роботи надіслати в особисті повідомлення у вайбер або на електронну адресу)

Алгебра

Урок 25.05.22

Тема. "Повторення. "Степінь з цілим показником. Квадратні корені. Квадратні рівняння."

👉І. Усно.

👉ІІІ. Домашнє завдання.

Повторити п.8, с.53; п.9, с.61; п.12, с.88; п.15, с.115; п.16, с.122; п.18, с.141; п.19, с.148. Письмово виконати тестові завдання.

Геометрія

Урок 27.05.22

Тема. "Повторення. Підготовка до річної контрольної роботи"

👉І. Усно.

Повторення вивченого. Таблиці с.179-183.

2. На рис. 2 ABCD — прямокутник. Знайдіть х і у.3. Знайдіть висоту й бічну сторону рівнобедреної трапеції з основами 2 і 8 та гострим кутом α.

4. У рівнобедреній трапеції кут при основі дорівнює 135°, менша основа і бічна сторона — відповідно 8 і 10. Знайдіть середню лінію трапеції.

8. Визначте довжину кола, якщо площа його круга дорівнює 48π см2.

Алгебра

Урок 25.05.22

Тема. "Повторення. Властивості та графіки функцій у=k/х; у=х2; у= √х"

👉І. Усно.

1. Повторити п.10, с.69; п.11, с.83; п.17, с.132. Контрольні запитання 1-8, с.73. Таблиця с.72. Контрольні запитання 1-5, с.85. Таблиця с.85. Контрольні запитання 1-7, с.135. Таблиця с.134.

2. Натисніть на посилання. Продивіться відео.

https://youtu.be/uIRqu1PnbOg

3. Логічна вправа:

Який запис пропущено?Раціональний дрібКвадрат числау = х2Квадратний корінь?

4. Запитання.Який із графіків, зображених на рисунку, є графіком функції y = x2

4. Запитання.

Який із графіків, зображених на рисунку, є графіком

функції y = x2

👉ІІ. Письмово.

1. Не виконуючи побудови графіка функції у = 5/х, визначте, які з даних точок належать графіку цієї функції:варіанти відповідей А(- 1; 5) В(- 5; -1) С(2,5; -2) D(- 2; -2,5)

Геометрія

Урок 24.05.22

Тема. "Повторення. Многокутники та їх площі"

👉І. Усно.

1. Повторити п.20-24, с.146-178. Контрольні запитання 1-8, с.178. Таблиця с.183.

👉ІІ. Письмово.

👉ІІІ. Домашнє завдання.

Повторити п. 20 - 24.Тестові завдання №1 (1-5), с.178

Алгебра

Урок 23.05.22

Тема. "Повторення. Тотожні перетворення раціональних виразів"

👉І. Усно.

1. Яка послідовність дій у виразі ?2. Прокоментуйте виконання дій у виразі .1) ; 2) ; 3) .Відповідь. .

👉ІІ. Письмово.

Конспект 1.Раціональні вирази. Раціональні рівнянняЦілі вирази Дробові ви рази Цілі рівняння = 2 Дробові рівняння = 2

Конспект

1.

Раціональні вирази.

Раціональні рівняння

Цілі вирази

Дробові ви рази

Цілі рівняння

= 2

Дробові рівняння = 2

2. Дробово-раціональне рівняння.

ОДЗ: значення змінної, при яких існують вирази в обох частинах рівняння.

Геометрія

Урок 20.05.22

Тема. "Повторення. Теорема Піфагора. Розвязування прямокутних трикутників"

👉І. Усно.

1. Повторити п.15-19, с.110-138.

👉ІІ. Письмово.

👉ІІІ. Домашнє завдання.

Контрольні запитання 1-6, с.142. Тестові завдання №1 (1-5), №2 (1-5).

Алгебра

Онлайн урок 18.05.22.

Тема: "Квадратний тричлен. Розв'язування задач за допомогою квадратних рівнянь"

👉І. Усно.

1. Підручник. Повторити п.21-23, с.166-183.

2. На рис. 2 ABCD — прямокутник. Знайдіть х і у.

3. Знайдіть висоту й бічну сторону рівнобедреної трапеції з основами 2 і 8 та гострим кутом α.

Який запис пропущено?
Раціональний дріб
Квадрат числа
у = х2
Квадратний корінь
?

4. Запитання.

Який із графіків, зображених на рисунку, є графіком
функції y = x2

1. Не виконуючи побудови графіка функції у = 5/х, визначте, які з даних точок належать графіку цієї функції:
варіанти відповідей

А(- 1; 5)

В(- 5; -1)

С(2,5; -2)

D(- 2; -2,5)

1. Яка послідовність дій у виразі ?
2. Прокоментуйте виконання дій у виразі .
1) ; 2) ; 3) .
Відповідь. .

Конспект
1.
Раціональні вирази.

Раціональні рівняння

Цілі вирази

Дробові ви рази

Цілі рівняння
= 2
Дробові рівняння = 2